Далее: 4. Матрицы и определители
Вверх: I. Элементы аналитической геометрии
Назад: 2. Прямая на плоскости
Вопросы теории. Система линейных уравнений и ее решение.
Совместные и несовместные системы линейных уравнений. Равносильные системы.
Однородная система. Совместность однородных систем линейных уравнений.
Свойства решений однородной системы линейных уравнений. Основная и
расширенная матрицы системы линейных уравнений. Элементарные преобразования
системы линейных уравнений. Теорема об элементарных преобразованиях.
Метод Гаусса решения систем линейных уравнений.
Образцы решения задач
Задача 1. Известно, что
 и
и
 - решения системы
- решения системы
Не решая системы, укажите еще одно ненулевое ее решение, отличное от данных.
Решение. Система однородна, поэтому всякая линейная комбинация
 ее решений
ее решений
 и
и
 будет снова
решением. Выбирая, например,
будет снова
решением. Выбирая, например,  имеем
имеем
 . Непосредственной проверкой убеждаемся
в том, что полученная комбинация действительно является решением системы.
. Непосредственной проверкой убеждаемся
в том, что полученная комбинация действительно является решением системы.
Задача 2. Найдите общее и укажите какое-нибудь частное
решение системы
Решение. Решим систему методом Гаусса.
Расширенная матрица системы имеет вид
Сначала исключим переменную 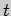 из всех уравнений, кроме первого. Для этого
надо воспользоваться первой строкой: для вычисления преобразованной второй
строки прибавим первую строку ко второй, для вычисления преобразованной
третьей строки - к третьей прибавим первую, для вычисления
четвертой строки - к четвертой прибавим первую. Матрица примет вид
Исключив переменную
из всех уравнений, кроме первого. Для этого
надо воспользоваться первой строкой: для вычисления преобразованной второй
строки прибавим первую строку ко второй, для вычисления преобразованной
третьей строки - к третьей прибавим первую, для вычисления
четвертой строки - к четвертой прибавим первую. Матрица примет вид
Исключив переменную  из всех уравнений, кроме третьего, имеем:
В полученной матрице вторая и четвертая строки одинаковы; это значит, что
в соответствующей ей системе уравнений, равносильной исходной, два уравнения
совпадают. Следовательно, одну из совпадающих строк можно вычеркнуть.
Матрица принимает вид
Исключая переменную
из всех уравнений, кроме третьего, имеем:
В полученной матрице вторая и четвертая строки одинаковы; это значит, что
в соответствующей ей системе уравнений, равносильной исходной, два уравнения
совпадают. Следовательно, одну из совпадающих строк можно вычеркнуть.
Матрица принимает вид
Исключая переменную  из всех уравнений, кроме второго, получаем
Ставя в соответствие этой матрице систему уравнений и выражая из нее
базисные переменные
из всех уравнений, кроме второго, получаем
Ставя в соответствие этой матрице систему уравнений и выражая из нее
базисные переменные  через свободную переменную
через свободную переменную 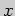 , получим
общее решение
Полагая, например,
, получим
общее решение
Полагая, например,  имеем частное решение:
имеем частное решение:

Задачи для самостоятельного решения
1. Даны два частных решения однородной системы. Не решая систему, укажите еще
два ненулевых частных решения той же системы, отличных от данных. Есть ли в
задаче избыточные данные?
2. Найдите общие решения систем, указанных в задаче 1.
3. Найдите общее и укажите какое-нибудь частное решение системы
Далее: 4. Матрицы и определители
Вверх: I. Элементы аналитической геометрии
Назад: 2. Прямая на плоскости
ЯГПУ, Центр информационных технологий обучения
27.03.2007
![]() и
и
![]() - решения системы
- решения системы


![$\displaystyle \left[ \begin{array}{rrrr\vert r}
x&y&z&t\\
\hline
1&2&-3&1&0\\
-1&1&-1&-1&-6\\
2&-1&1&-1&-1\\
2&2&-3&-1&-7
\end{array} \right].
$](img197.png)
![$\displaystyle \left[ \begin{array}{rrrr\vert r}
1&2&-3&1&0\\
0&3&-4&0&-6\\
3&1&-2&0&-1\\
3&4&-6&0&-7
\end{array} \right].
$](img198.png)
![$\displaystyle \left[ \begin{array}{rrrr\vert r}
-5&0&1&1&2\\
-9&0&2&0&-3\\
3&1&-2&0&-1\\
-9&0&2&0&-3
\end{array} \right].
$](img200.png)
![$\displaystyle \left[ \begin{array}{rrrr\vert r}
-5&0&1&1&2\\
-9&0&2&0&-3\\
3&1&-2&0&-1
\end{array} \right].
$](img201.png)
![$\displaystyle \left[ \begin{array}{rrrr\vert r}
-0,5&0&0&1&3,5\\
-9&0&2&0&-3\\...
...\vert r}
-0,5&0&0&1&3,5\\
-4,5&0&1&0&-1,5\\
-6&1&0&0&-4
\end{array} \right].
$](img203.png)



