Далее: Описание этапов проведения лабораторной Вверх: Лабораторная работа № 4 Назад: Лабораторная работа № 4

Теоретический аспект

При решении обыкновенных дифференциальных уравнений первого порядка, часто встречающихся при построении математических моделей различных явлений и процессов, нередка проблема невозможности или сложности решения данных уравнений.

В подобных ситуациях для решения обыкновенных дифференциальных уравнений первого порядка используют рассматриваемые в рамках данной лабораторной работы численные методы. Суть применяемых численных методов заключается в том, что для заданного обыкновенного дифференциального уравнения вида ${y}' = f\left( {x,y\left( x \right)} \right)$ или $\frac{dy}{dx} = f(x,y)$ с начальными условиями, характеризующими координаты точки $\left( {a_0 ,y\left( {a_0 } \right)} \right)$ на некотором отрезке $[a_0 ,b_0 ]$, необходимо рассчитать приближенное значение функции $y\left( {b_0 } \right)$ в точке с координатами $\left( {b_0 ,y\left( {b_0 } \right)} \right)$. Осуществляется деление данного отрезка на определенное количество равных меньших отрезков или шагов в зависимости от заданного значения количества шагов $s_\alpha$ или значения фиксированного шага $h_\alpha$, расчет приближенного значения функции со значением абсциссы конечной точки на каждом из полученных отрезков, при этом приближенное значение функции $y\left( {b_0 } \right)$ в точке с координатами $\left( {b_0 ,y\left( {b_0 } \right)} \right)$ определяется как значение функции со значением абсциссы конечной точки последнего из полученных отрезков.

Рассмотрим логические основы реализации методов Эйлера, Рунге-Кутта второго и четвертого порядков для выполнения приближенных решений обыкновенных дифференциальных уравнений первого рода в зависимости от различных значений $a_0$, $y\left( {a_0 } \right)$, $b_0$, $s_\alpha$ или $h_\alpha$, заложенных в программу "APROXDFE".

Метод Эйлера

Исходя из уравнения касательной, проходящей из точки с координатами $\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$ к графику исходной функции $y\left( x \right)$, то есть $y_1 \left( {x_N } \right) = y(x_{N - 1} ) + {y}'(x_{N - 1} ) \cdot (x_N - x_{N - 1} )$, учитывая, что ${y}'(x_N ) = f\left( {x_N ,f\left( {x_N } \right)} \right)$ или ${y}'(x_{N - 1} ) = f\left( {x_{N - 1} ,f\left( {x_{N - 1} } \right)} \right)$ и $x_N - x_{N - 1} = h_\alpha$, получим соотношение: $\Delta y\left( {x_N } \right) = y_1 \left( {x_N } \right) - y(x_{N - 1} ) = {y}... ...} ) = f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right) \cdot h_\alpha$.

Таким образом, в методе Эйлера вычисление приближенного значения координат точки исходной функции с координатами $\left( {x_N ,y\left( {x_N } \right)} \right)$, исходя из приближенных значений координат точки $\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$ исходной функции, осуществляется согласно следующим соотношениям:

$$y\left( {x_N } \right) = y\left( {x_{N - 1} } \right) + \Del... ...N - 1} ,y\left( {x_{N - 1} } \right)} \right) \cdot h_\alpha ,$$

$$x_N = x_{N - 1} + h_\alpha .$$

Полученные соотношения можно получить и другими способами.

Например, используя формулировку вычисления определенного интеграла для функции $f\left( {x,y\left( x \right)} \right)$, учитывая, что ${y}'(x_N ) = f\left( {x_N ,y\left( {x_N } \right)} \right)$ или ${y}'(x_{N - 1} ) = f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$ и $x_N - x_{N - 1} = h_\alpha$, можно получить следующее соотношение:

$$\Delta y\left( {x_N } \right) = y\left( {x_N } \right) - y(x... ...f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)dx} .$$

По формуле прямоугольников получим, что

$$\Delta y\left( {x_N } \right) = y\left( {x_N } \right) - y(x... ...t( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)h_\alpha .$$

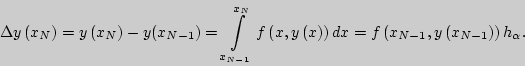
Тогда вычисление приближенных значений координат точки исходной функции с координатами $\left( {x_N ,y\left( {x_N } \right)} \right)$, исходя из приближенных значений координат точки $\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$, по методу Эйлера осуществляется согласно следующим соотношениям:

$$y\left( {x_N } \right) = y\left( {x_{N - 1} } \right) + \Del... ...N - 1} ,y\left( {x_{N - 1} } \right)} \right) \cdot h_\alpha ,$$

$$x_N = x_{N - 1} + h_\alpha .$$

Также соотношения метода Эйлера можно получить как частный случай методов Рунге-Кутта.

В методах Рунге-Кутта определенный интеграл определяется в виде интерполяционного многочлена согласно следующему соотношению:

$$\begin{array}{l} y\left( {x_N } \right) = y\left( {x_{N - 1... ...S {p_J \cdot K_J \left( {h_\alpha } \right)} , \\ \end{array}$$

где $p_J$ - коэффициенты, зависящие от S; $K_J \left( {h_\alpha } \right)$ - функции, зависящие от вида подынтегральной функции $f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$ и значения фиксированного шага $h_\alpha$.

В общем случае значения $p_J$ и $K_J \left( {h_\alpha } \right)$ определяются согласно следующим соотношениям:

$$K_1 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right),$$

$$K_2 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{... ...) + \beta _{21} \cdot K_1 \left( {h_\alpha } \right)} \right),$$

$$K_3 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{... ...) + \beta _{32} \cdot K_2 \left( {h_\alpha } \right)} \right),$$
................................. ................................. .............

$$K_S \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{... ...{S,S - 1} \cdot K_{S - 1} \left( {h_\alpha } \right)} \right).$$

Значения $p_J$, $\alpha _S$ и $\beta _{S,S - 1}$ получают из соображений высокой точности вычислений.

Если $p_1 = 1$ и $K_1 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$, то получим соотношение:

$$\begin{array}{l} y\left( {x_N } \right) = y\left( {x_{N - 1... ...N - 1} ,y\left( {x_{N - 1} } \right)} \right). \\ \end{array}$$

Таким образом, метод Эйлера является методом Рунге-Кутта первого порядка.

В данной лабораторной работе метод Эйлера ("METHOD OF EULER") имеет следующую реализацию:

Итерация с индексом $''N'' \quad \left( {N \ge 1} \right)$:

На искомом отрезке $\left[ {a_0 ,b_0 } \right]$ при соблюдении условия $a_0 < b_0$, исходя из вводимого или рассчитанного значения фиксированного шага $h_\alpha ^E$ (при вводимом значении количества шагов $s_\alpha ^E$ по формуле $h_\alpha ^E = \frac{b_0 - a_0 }{s_\alpha ^E })$, выбирается абсцисса точки исходной функции с координатами $\left( {x_N^E ,y\left( {x_N^E } \right)} \right)$, то есть $x_N^E$, согласно следующему соотношению: $x_N^E = x_{N - 1}^E + h_\alpha ^E$.

Осуществляется вычисление приближенного значения ординаты точки исходной функции с координатами $\left( {x_N^E ,y\left( {x_N^E } \right)} \right)$, то есть $y\left( {x_N^E } \right)$, согласно следующим соотношениям:

$$y\left( {x_N^E } \right) = y\left( {x_{N - 1}^E } \right) + ... ...f\left( {x_{N - 1}^E ,y\left( {x_{N - 1}^E } \right)} \right),$$

$$x_N^E = x_{N - 1}^E + h_\alpha ^E .$$

Если достигнута истинность выражения $x_N^E \ge b_0$, то итерации прекращаются, количество шагов итераций $s_\alpha ^E = N$, и приближенное значение исходной функции $y\left( {b_0 } \right)$ в точке с координатами $\left( {b_0 ,y\left( {b_0 } \right)} \right)$ определятся согласно соотношению $y\left( {b_0^E } \right) = y\left( {x_N^E } \right)$.

Если $x_N^E < b_0$, то осуществляется переход к следующей итерации.

Метод Рунге-Кутта 2-го порядка

В методе Рунге-Кутта второго порядка имеем следующие соотношения:

Если $p_1 = 0$, то $K_1 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$;

Если $p_2 = 1$, то $\alpha _2 = \frac{1}{2}$, $\beta _{21} = \frac{1}{2}$ и

$$\begin{array}{l} K_2 \left( {h_\alpha } \right) = h_\alpha ... ...\left( {x_{N - 1} } \right)} \right)} \right). \\ \end{array}$$

В итоге получим соотношение:

$$\begin{array}{l} y\left( {x_N } \right) = y\left( {x_{N - 1... ...\left( {x_{N - 1} } \right)} \right)} \right). \\ \end{array}$$

Тогда вычисление приближенных значений координат точки исходной функции с координатами $\left( {x_N ,y\left( {x_N } \right)} \right)$, исходя из приближенных значений координат точки $\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$, по методу Рунге-Кутта второго порядка осуществляется согласно следующим соотношениям:

$$x_{{\left( {2N - 1} \right)} \mathord{\left/ {\vphantom {{\l... ...ern-\nulldelimiterspace} 2} = x_{N - 1} + \frac{h_\alpha }{2},$$

$$y\left( {x_{{\left( {2N - 1} \right)} \mathord{\left/ {\vpha... ...dot f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right),$$

$$y\left( {x_N } \right) = y\left( {x_{N - 1} } \right) + \Del... ... 2}} \right. \kern-\nulldelimiterspace} 2} } \right)} \right),$$

$$x_N = x_{N - 1} + h_\alpha .$$

В данной лабораторной работе метод Рунге-Кутта второго порядка ("METHOD OF RUNGA-KUTTA 2") имеет следующую реализацию:

Итерация с индексом $''N'' \quad \left( {N \ge 1} \right)$:

На искомом отрезке $\left[ {a_0 ,b_0 } \right]$ при соблюдении условия $a_0 < b_0$, исходя из вводимого или рассчитанного значения фиксированного шага $h_\alpha ^{RK2}$ (при вводимом значении количества шагов $s_\alpha ^{RK2}$ по формуле $h_\alpha ^{RK2} = \frac{b_0 - a_0 }{s_\alpha ^{RK2} })$, выбирается абсцисса точки исходной функции с координатами $\left( {x_N^{RK2} ,y\left( {x_N^{RK2} } \right)} \right)$, то есть $x_N^{RK2}$, согласно следующему соотношению: $x_N^{RK2} = x_{N - 1}^{RK2} + h_\alpha ^{RK2}$.

Осуществляется вычисление приближенного значения ординаты точки исходной функции с координатами $\left( {x_N^{RK2} ,y\left( {x_N^{RK2} } \right)} \right)$, то есть $y\left( {x_N^{RK2} } \right)$, согласно следующим соотношениям:

$$x_{{\left( {2N - 1} \right)} \mathord{\left/ {\vphantom {{\l... ...pace} 2}^{RK2} = x_{N - 1}^{RK2} + \frac{h_\alpha ^{RK2} }{2},$$

$$y\left( {x_{{\left( {2N - 1} \right)} \mathord{\left/ {\vpha... ...{2} \cdot f\left( {x_{N - 1}^{RK2} ,y_{N - 1}^{RK2} } \right),$$

$$y\left( {x_N^{RK2} } \right) = y\left( {x_{N - 1}^{RK2} } \r... ...t)} 2}} \right. \kern-\nulldelimiterspace} 2}^{RK2} } \right),$$

$$x_N^{RK2} = x_{N - 1}^{RK2} + h_\alpha ^{RK2} .$$

Если достигнута истинность выражения $x_N^{RK2} \ge b_0^{RK2}$, то итерации прекращаются, количество шагов итераций $s_\alpha ^{RK2} = N$, и приближенное значение исходной функции $y\left( {b_0 } \right)$ в точке с координатами $\left( {b_0 ,y\left( {b_0 } \right)} \right)$ определятся согласно соотношению $y\left( {b_0^{RK2} } \right) = y\left( {x_N^{RK2} } \right)$.

Если $x_N^{RK2} < b_0$, то осуществляется переход к следующей итерации.

Метод Рунге-Кутта 4-го порядка

В методе Рунге-Кутта четвертого порядка имеем следующие соотношения:

Если $p_1 = \frac{1}{6}$, то $K_1 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$.

Если $p_2 = \frac{1}{3}$, то $\alpha _2 = \frac{1}{2}$, $\beta _{21} = \frac{1}{2}$ и

$$\begin{array}{l} K_2 \left( {h_\alpha } \right) = h_\alpha ... ...\left( {x_{N - 1} } \right)} \right)} \right). \\ \end{array}$$

Если $p_3 = \frac{1}{3}$, то $\alpha _3 = \frac{1}{2}$, $\beta _{31} = 0$, $\beta _{32} = \frac{1}{2}$ и

$$K_3 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{... ...) + \frac{1}{2} \cdot K_2 \left( {h_\alpha } \right)} \right).$$

Если $p_4 = \frac{1}{6}$, то $\alpha _4 = 1$, $\beta _{41} = 0$, $\beta _{42} = 0$, $\beta _{43} = 1$ и

$$K_4 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{... ...x_{N - 1} } \right) + K_3 \left( {h_\alpha } \right)} \right).$$

В итоге получим соотношение:

$$\begin{array}{l} y\left( {x_N } \right) = y\left( {x_{N - 1... ...ht) + K_4 \left( {h_\alpha } \right)} \right). \\ \end{array}$$

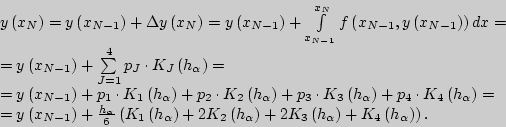
Тогда вычисление приближенного значения координат точки исходной функции с координатами $\left( {x_N ,y\left( {x_N } \right)} \right)$ исходя из приближенных значений координат точки $\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right)$ по методу Рунге-Кутта четвертого порядка осуществляется согласно следующим соотношениям:

$$K_1 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{N - 1} ,y\left( {x_{N - 1} } \right)} \right),$$

$$x_{{\left( {2N - 1} \right)} \mathord{\left/ {\vphantom {{\l... ...ern-\nulldelimiterspace} 2} = x_{N - 1} + \frac{h_\alpha }{2},$$

$$K_2 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{... ...} \right) + \frac{K_1 \left( {h_\alpha } \right)}{2}} \right),$$

$$K_3 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_{... ...} \right) + \frac{K_2 \left( {h_\alpha } \right)}{2}} \right),$$

$$x_N = x_{N - 1} + h_\alpha ,$$

$$K_4 \left( {h_\alpha } \right) = h_\alpha \cdot f\left( {x_N... ...x_{N - 1} } \right) + K_3 \left( {h_\alpha } \right)} \right),$$

$$y\left( {x_N } \right) = y\left( {x_{N - 1} } \right) + \Del... ... {h_\alpha } \right) + K_4 \left( {h_\alpha } \right)} \right)$$

В данной лабораторной работе метод Рунге-Кутта четвертого порядка ("METHOD OF RUNGA-KUTTA 4") имеет следующую реализацию:

Итерация с индексом $''N'' \quad \left( {N \ge 1} \right)$:

На искомом отрезке $\left[ {a_0 ,b_0 } \right]$ при соблюдении условия $a_0^{RK4} < b_0^{RK4}$, исходя из вводимого или рассчитанного значения фиксированного шага $h_\alpha ^{RK4}$ (при вводимом количестве шагов $s_\alpha ^{MR}$ по формуле $h_\alpha ^{RK4} = \frac{b_0 - a_0 }{s_\alpha ^{RK4} })$, выбирается абсцисса точки исходной функции с координатами $\left( {x_N^{RK4} ,y\left( {x_N^{RK4} } \right)} \right)$, то есть $x_N^{RK4}$, согласно следующему соотношению: $x_N^{RK4} = x_{N - 1}^{RK4} + h_\alpha ^{RK4}$.

Осуществляется вычисление приближенных значений ординат точки исходной функции с координатами $\left( {x_N^{RK4} ,y\left( {x_N^{RK4} } \right)} \right)$, то есть $y\left( {x_N^{RK4} } \right)$, согласно соотношениям:

$$K_{1N} \left( {h_\alpha ^{RK4} } \right) = h_\alpha ^{RK4} \... ...{x_{N - 1}^{RK4} ,y\left( {x_{N - 1}^{RK4} } \right)} \right),$$

$$x_{{\left( {2N - 1} \right)} \mathord{\left/ {\vphantom {{\l... ...pace} 2}^{RK4} = x_{N - 1}^{RK4} + \frac{h_\alpha ^{RK4} }{2},$$

$$K_{2N} \left( {h_\alpha ^{RK4} } \right) = h_\alpha ^{RK4} \... ...+ \frac{K_{1N} \left( {h_\alpha ^{RK4} } \right)}{2}} \right),$$

$$K_{3N} \left( {h_\alpha ^{RK4} } \right) = h_\alpha ^{RK4} \... ...+ \frac{K_{2N} \left( {h_\alpha ^{RK4} } \right)}{2}} \right),$$

$$x_N^{RK4} = x_{N - 1}^{RK4} + h_\alpha ^{RK4} ,$$              $$K_{4N} \left( {h_\alpha ^{RK4} } \right) = h_\alpha ^{RK4} \... ...} \right) + K_{3N} \left( {h_\alpha ^{RK4} } \right)} \right),$$

$$\begin{array}{l} y\left( {x_N^{RK4} } \right) = y\left( {x_... ...N} \left( {h_\alpha ^{RK4} } \right)} \right). \\ \end{array}$$

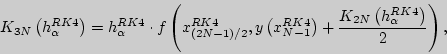
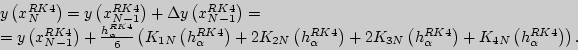
Если достигнута истинность выражения $x_N^{RK4} \ge b_0$, то итерации прекращаются, количество шагов итераций $s_\alpha ^{RK4} = N$, и приближенное значение исходной функции $y\left( {b_0 } \right)$ в точке с координатами $\left( {b_0 ,y\left( {b_0 } \right)} \right)$ определятся согласно соотношению $y\left( {b_0^{RK4} } \right) = y\left( {x_N^{RK4} } \right)$.

Если $x_N^{RK4} < b_0$, то осуществляется переход к следующей итерации.

Далее: Описание этапов проведения лабораторной Вверх: Лабораторная работа № 4 Назад: Лабораторная работа № 4