Далее: §8. Схема
Бернулли
Вверх: Глава II.
Случайные события
Назад: §6. Условные
вероятности
Если событие 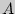 может наступить только при появлении одного
из
несовместных
событий (гипотез)
может наступить только при появлении одного
из
несовместных
событий (гипотез)  , то вероятность события
, то вероятность события
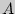 вычисляется по формуле полной вероятности:
вычисляется по формуле полной вероятности:
 ,
где
,
где  -
вероятность гипотезы
-
вероятность гипотезы  ,
,

 -
условная вероятность события
-
условная вероятность события 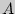 при выполнении гипотезы
при выполнении гипотезы  (
(
 .
.
Проиллюстрируем формулу полной вероятности на графе с выделенной
вершиной:
Рис. 17
Полная вероятность события 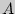 равна весу всего
вероятностного
графа с
гипотезами.
равна весу всего
вероятностного
графа с
гипотезами.
С формулой полной вероятности тесно связана формула Байеса. Если до
опыта
вероятности гипотез были  ,
,  ,
...,
,
...,  , а в результате
опыта появилось событие
, а в результате
опыта появилось событие 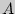 , то с учетом этого события
"новые", т.е. условные
вероятности гипотез вычисляются по формуле Байеса
, то с учетом этого события
"новые", т.е. условные
вероятности гипотез вычисляются по формуле Байеса
Формула Байеса дает возможность "пересмотреть" вероятность гипотез с
учетом наблюдавшегося результата опыта. Условная вероятность
 может находиться как отношение веса ветви,
проходящей через вершину,
соответствующую гипотезе
может находиться как отношение веса ветви,
проходящей через вершину,
соответствующую гипотезе  , к весу всего
вероятностного
графа.
, к весу всего
вероятностного
графа.
Пример 31. На заводе, изготовляющем болты, первая машина
производит
25%, вторая - 35%, третья - 40% всех изделий. В их продукции брак
составляет соответственно 5, 4 и 2%.
а) Какова вероятность того, что случайно выбранный болт дефектный?
б) Случайно выбранный из продукции болт оказался дефектным. Какова
вероятность того, что он был произведен первой, второй, третьей
машиной?
Решение. Пусть событие 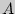 = {выбрать дефектный болт}.
= {выбрать дефектный болт}.
Выдвигаем три гипотезы:
 ={болт изготовлен первой машиной},
={болт изготовлен первой машиной},  =0,25,
=0,25,
 =0,05;
=0,05;
 ={болт изготовлен второй машиной},
={болт изготовлен второй машиной},  =0,35,
=0,35,
 =0,04;
=0,04;
 ={болт изготовлен третьей машиной},
={болт изготовлен третьей машиной},  =0,4,
=0,4,
 =0,02.
=0,02.
Рис. 18
а)

б)

Пример 32. Студент подготовил к экзамену 20 билетов из 25. В
каком
случае шансы взять известный билет больше - когда студент пришел на
экзамен
первым или вторым?
Решение.
 Найдем вероятность
Найдем вероятность  взять известный билет, придя на экзамен вторым, учитывая, что первый
может
взять как известный, так и неизвестный второму билет.
взять известный билет, придя на экзамен вторым, учитывая, что первый
может
взять как известный, так и неизвестный второму билет.
Рис. 19
Пример 33. Наудачу выбираем колоду, а из нее карту. В каком
случае
вероятность достать туз больше: если выбирать карту из двух колод,
содержащих по 32 и 52 карты, или выбирать карту из трех колод в 36 карт
и
одной в 52?
Решение. Пусть событие 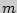 = { достать туз}.
= { достать туз}.
Рис. 20
 , следовательно, в первом
случае вероятность достать туз меньше, чем во втором.
, следовательно, в первом
случае вероятность достать туз меньше, чем во втором.
Пример 34. В каждой из трех урн содержится по одному белому и
одному черному шару. Из первой урны во вторую переложили один шар, из
второй
пополненной урны в третью тоже переложили один шар, а затем из третьей
урны
наудачу извлекли один шар. Какова вероятность извлечь белый шар из
третьей
пополненной урны?
Решение.
Рис. 21
Какие гипотезы использовались в решении этой задачи?
Пример 35. Предположим, что 5 мужчин из 100 и 25 женщин из
10000
являются дальтониками. Наугад выбранное лицо страдает дальтонизмом.
Какова
вероятность, что это мужчина?
Решение.
Рис. 22
Вопросы для самоконтроля
- Какие события образуют полную группу?
- Что можно сказать о вероятностях событий, образующих полную
группу событий?
- Получите формулу для вычисления полной вероятности.
- В каком случае применяется формула полной вероятности? Приведите
примеры.
- Интерпретация формулы полной вероятности на графах.
- Поясните смысл выражения "условная вероятность гипотезы".
- Докажите формулу Байеса.
- Как с помощью вероятностного графа можно "пересматривать"
вероятности
гипотез?
Задачи
- I 61. Одна кость из полного набора домино утеряна. Какова
вероятность того, что извлеченная из оставшихся кость "подходит" к
утерянной?
- 62. Имеются три урны: в первой - 3 белых и 2 черных, во
второй - 2
белых и
3 черных, в третьей - 5 белых шаров. Наугад выбирается урна и из нее
извлекается один шар. Этот шар оказался белым. Найдите вероятность
того, что
шар вынут из первой урны.
- 63. В первой урне 2 белых и 5 черных шаров, во второй - 3
белых и 4
черных.
Из первой урны один шар переложен во вторую, после чего из второй урны
извлекают один шар. Какова вероятность того, что этот шар белый?
- 64. В двух пакетах по 20 конфет одинаковой формы, в первом
пакете 5
конфет с
начинкой, а во втором - 8. Наугад выбранная конфета оказалась с
начинкой.
Найдите вероятность того, что она была вынута из второго пакета.
- 65. Имеются три колоды в 32 карты, две - в 36 и одна - в
52. Выбираем
колоду и из нее одну карту. Какова вероятность того, что вынутая карта
окажется тузом?
- 66. Сборщик получил три коробки деталей, изготовленных
заводом 1, и
две
коробки деталей, изготовленных заводом 2. Вероятность того, что деталь
завода 1 стандартна, равна 0,9, а завода 2 - 0,8. Сборщик извлек
стандартную деталь из наудачу взятой коробки. Найдите вероятность того,
что
она изготовлена заводом №1.
- II 67. В первой урне содержатся один белый и один черный
шар, а во
второй - один белый и два черных шара. Найдите вероятность извлечения
белого шара, если:
- а) урна выбирается случайно и из нее извлекается шар;
- б) из каждой урны извлекли по одному шару и из них выбирается
шар;
- в) из первой урны переложили во вторую один шар, а затем из нее
извлекли шар.
- 68. В урну, содержащую
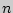 шаров, опущен
белый шар, после
чего наудачу
извлечен один шар. Найдите вероятность того, что извлеченный шар
окажется
белым.
шаров, опущен
белый шар, после
чего наудачу
извлечен один шар. Найдите вероятность того, что извлеченный шар
окажется
белым.
- III 69. Король Артур проводит рыцарский турнир, в котором
порядок
состязания определяется жребием. Среди восьми рыцарей, одинаково
искушенных
в ратном деле, два близнеца. Какова вероятность того, что они
встретятся в
поединке?
- 70. Преподаватель шутки ради предложил студенту
распределить по двум
урнам
два белых и один черный шар. Преподаватель выбирает наугад одну из урн
и
вынимает из нее шар: если шар будет белый, то студент получает зачет по
теории вероятностей. Каким образом студенту нужно распределить шары в
урнах,
чтобы иметь наибольшие шансы на получение зачета?
Далее: §8. Схема
Бернулли
Вверх: Глава II.
Случайные события
Назад: §6. Условные
вероятности
ЯГПУ, Центр информационных
технологий обучения
2006-03-04

![]() может наступить только при появлении одного
из
несовместных
событий (гипотез)
может наступить только при появлении одного
из
несовместных
событий (гипотез) ![]() , то вероятность события
, то вероятность события
![]() вычисляется по формуле полной вероятности:
вычисляется по формуле полной вероятности:
![]() ,
где
,
где ![]() -
вероятность гипотезы
-
вероятность гипотезы ![]() ,
,

![]() -
условная вероятность события
-
условная вероятность события ![]() при выполнении гипотезы
при выполнении гипотезы ![]() (
(
![]() .
.

![]() равна весу всего
вероятностного
графа с
гипотезами.
равна весу всего
вероятностного
графа с
гипотезами.
![]() ,
, ![]() ,
...,
,
..., ![]() , а в результате
опыта появилось событие
, а в результате
опыта появилось событие ![]() , то с учетом этого события
"новые", т.е. условные
вероятности гипотез вычисляются по формуле Байеса
, то с учетом этого события
"новые", т.е. условные
вероятности гипотез вычисляются по формуле Байеса

![]() может находиться как отношение веса ветви,
проходящей через вершину,
соответствующую гипотезе
может находиться как отношение веса ветви,
проходящей через вершину,
соответствующую гипотезе ![]() , к весу всего
вероятностного
графа.
, к весу всего
вероятностного
графа.
![]() = {выбрать дефектный болт}.
= {выбрать дефектный болт}.
![]() ={болт изготовлен первой машиной},
={болт изготовлен первой машиной}, ![]() =0,25,
=0,25,
![]() =0,05;
=0,05;
![]() ={болт изготовлен второй машиной},
={болт изготовлен второй машиной}, ![]() =0,35,
=0,35,
![]() =0,04;
=0,04;
![]() ={болт изготовлен третьей машиной},
={болт изготовлен третьей машиной}, ![]() =0,4,
=0,4,
![]() =0,02.
=0,02.

![]()
![]()
![]() Найдем вероятность
Найдем вероятность ![]() взять известный билет, придя на экзамен вторым, учитывая, что первый
может
взять как известный, так и неизвестный второму билет.
взять известный билет, придя на экзамен вторым, учитывая, что первый
может
взять как известный, так и неизвестный второму билет.

![]() = { достать туз}.
= { достать туз}.

![]() , следовательно, в первом
случае вероятность достать туз меньше, чем во втором.
, следовательно, в первом
случае вероятность достать туз меньше, чем во втором.


