Далее: 6.  Первое и второе Вверх: 5.  Второе начало термодинамики Назад: 5.3.  Принцип энтропии

5.4.  Второе начало термодинамики для
необратимых процессов

Для обобщения второго начала термодинамики на случай необратимых процессов рассмотрим две задачи.

1. Определить, каким образом изменяется энтропия газа (увеличивается или уменьшается) при его адиабатическом расширении в пустоту.

Рис. 11 

Решение. Рассмотрим адиабатическиизолированный сосуд, разделенный невесомым поршнем на две части, одна из которых заполнена газом, а в другой создан идеальный вакуум. Вначале поршень зафиксирован. В какой-то момент времени его освобождают и он, двигаясь без трения, позволяет газу заполнить весь сосуд (рис. 11). Как изменяется при этом энтропия системы?

Расширяясь, газ не совершает работы, так как внешняя сила со стороны пустой части сосуда на него не действует, сила трения отсутствует, увеличения кинетической энергии поршня не происходит (по условию - он невесомый). Теплообмен в системе также отсутствует, поскольку сосуд адиабатически изолирован. Тогда, в соответствии с первым началом термодинамики, внутренняя энергия газа не изменяется. Заметим попутно, что, поскольку для идеального газа это означает постоянство температуры, мы имеем пример необратимого процесса, который одновременно оказывается изотермическим и адиабатическим, что для обратимых процессов невозможно.

Под изменением энтропии как функции состояния нужно понимать разность ее значений для конечного и начального состояний, поскольку способ их достижения неважен. Использовать в данной задаче для оценки изменения энтропии в промежуточных состояниях определение (12) нельзя, так как рассматриваемый процесс необратим. Однако начальное и конечное состояния являются равновесными, поэтому можно вычислить разность значений энтропии, если заменить наш процесс на обратимый с теми же начальным и конечным состояниями. Будем считать, что на поршень действует внешняя сила, равная произведению его площади на давление газа и направленная в сторону газа. В этом случае газ, медленно расширяясь, совершает положительную работу. Тогда для того, чтобы внутренняя энергия имела одинаковое значение в начале и в конце процесса, нужно обеспечить подвод к системе тепла в количестве, равном произведенной работе.

При этом, в соответствии с (12), энтропия газа будет возрастать. Возрастание будет монотонным, так как поршень можно зафиксировать в любом промежуточном положении и, рассматривая полученное состояние как конечное, провести те же рассуждения. Заметим также, что наличие в описанном опыте невесомого и скользящего без трения поршня (весьма нереальная модель) необязательно, так как те же начальное и конечное состояния будут у газа при истечении в вакуум через кран. Поршень введен в рассмотрение лишь из соображений наглядности.

2. Два тела с различными температурами приведены в тепловой контакт при отсутствии внешних воздействий. Определить, как изменяется (увеличивается или уменьшается) энтропия системы в процессе теплообмена.

Решение. При тепловом контакте в отсутствие внешних воздействий, как мы знаем из опыта, тепло передается от тела с большей температурой к телу с меньшей температурой. Начальное состояние каждого из тел является равновесным. Промежуточные состояния неравновесны как для системы в целом, так и для каждого из тел в отдельности, поскольку выравнивание температур из-за конечности теплопроводности будет происходить быстрее вблизи области контакта и все более медленно по мере удаления от нее. Поэтому внутри тел возникнет неравномерное распределение температуры по объему: у горячего тела температура будет спадать в направлении области контакта, у холодного - возрастать.

В конечном состоянии в равновесие приходит вся система. Таким образом, под изменением энтропии в процессе нужно понимать разность между энтропией конечного состояния и суммой значений энтропии тел в начальном состоянии.

Пусть начальные значения температур - $\ T_{1}<T_{2}$, конечное значение температуры в состоянии полного равновесия - $\ T\ :\ T_{1}\,<\,T\,<\,T_{2}$. Внутренняя энергия системы в целом не изменяется, так как система замкнута. Поскольку в самой системе по условию задачи никаких процессов, кроме теплообмена, не происходит, порции тепла, поглощенного первым телом и выделенного вторым телом, в соответствии с первым началом термодинамики равны увеличению (уменьшению) их внутренних энергий и, следовательно, равны между собой:

$$\Delta U_{1}\ =\ -\,\Delta U_{2}\;\;,\;\;\;\;\;\; Q_{1}\ =\ -\,Q_{2}\ =\ Q\;.$$

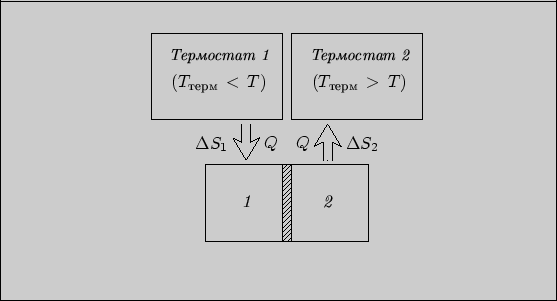
Рис. 12 

Далее, как и в предыдущей задаче, мысленнозаменим реальный процесс обратимым процессом с теми же начальным и конечным состояниями. Рассмотрим процесс, в котором тела не взаимодействуют между собой, но каждое из них взаимодействует с термостатом. Пусть первая система взаимодействует с термостатом, температура которого медленно возрастает от $T_{1}$ до $T$, а вторая - с термостатом, температура которого медленно спадает от $T_{2}$ до $T$ (рис. 12)⁵. "Медленность" процессов теплообмена здесь определяется условиями равномерности распределения температур в объемах всех рассматриваемых тел и равенства температур соответствующего тела и его термостата. При выполнении этих условий процесс будет обратимым.

Так как для данного модельного процесса начальное и конечное состояния совпадают соответственно с начальным и конечным состояниями реального процесса, суммарное изменение внутренних энергий двух тел равно нулю, как и в реальном процессе. Следовательно, поскольку никаких изменений, кроме теплообмена, в системе не происходит, поглощенное первым телом и отданное вторым телом тепло также равны между собой.

Первое тело вместе с теплом $Q$ поглощает от термостата энтропию

$$\Delta S_{1}\ =\ \sum \frac{\Delta Q_{i}}{T_{i}}\ >\ \frac{Q}{T}\;,$$

так как на протяжении всего процесса поглощения тепла первым телом температуры $T_{i}<T$. Второе тело отдает энтропию

$$-\,\Delta S_{2}\ =\ \sum \frac{\mid\Delta Q_{i}\mid}{T_{i}}\ <\ \frac{Q}{T}\;,$$

так как передача тепла от второго тела к термостату происходит при температурах $T_{i}>T$ (знак "$-$" указывает, что изменение энтропии второго тела отрицательно).

Таким образом, суммарное изменение энтропии в модельном процессе, равное изменению энтропии в реальном процессе, положительно:

$$\Delta S\ =\ \Delta S_{1}\,+\,\Delta S_{2}\ >\ 0$$

(увеличение энтропии первого тела больше, чем уменьшение энтропии второго тела).

Мы видим, что процесс выравнивания температур контактирующих тел при отсутствии внешних воздействий сопровождается возрастанием энтропии. Увеличение энтропии будет происходить монотонно. Это можно доказать, разбивая объем контактирующих тел в произвольном промежуточном состоянии на тонкие слои с примерно одинаковой температурой внутри каждого слоя и применяя к каждой паре соседних слоев проведенные выше рассуждения.

Обобщая результаты двух рассмотренных задач на случай произвольного необратимого процесса, сделаем следующее утверждение.

В любом необратимом процессе при отсутствии взаимодействия с окружающей средой установление равновесия сопровождается монотонным возрастанием энтропии.

Данное утверждение (закон возрастания энтропии) является одной из формулировок второго начала термодинамики для необратимых процессов. Другая формулировка, известная из школьного учебника, представляет собой обобщение постулата Клаузиуса на необратимые процессы:

При тепловом контакте тел с различными температурами тепло передается от горячего тела к холодному. Самопроизвольная передача тепла от холодного тела к горячему невозможна.

Как следует из решения второй задачи, постулат Клаузиуса соответствует закону возрастания энтропии.

В самом общем случае вклад в изменение энтропии за счет теплового взаимодействия, определяемый формулой (12) (он может быть как положительным, так и отрицательным), суммируется с вкладом за счет необратимости процесса (всегда положительным), и равенство (12) переходит в неравенство:

$$\Delta S\ \geq\ \frac{\Delta Q}{T}\;.$$ (13)

Вопросы и задачи

5.1. Можно ли утверждать, что обратимый изотермический процесс осуществляется при постоянном значении внутренней энергии? Можно ли утверждать, что обратимый адиабатический процесс осуществляется при постоянном значении энтропии?

5.2. Изобразите цикл Карно на диаграмме $(T,S)$: по оси ординат откладывается температура, по оси абсцисс - энтропия. Какой смысл имеет площадь под кривой процесса на этой диаграмме?

5.3. Два сосуда с различными газами соединены трубкой с краном. Показать, не пользуясь законом возрастания энтропии, что после открытия крана в процессе взаимной диффузии энтропия системы будет возрастать. Считать, что газы химически не взаимодействуют.

5.4. Обратимый цикл Карно осуществляется в системе, которая состоит из воды и находящегося в равновесии с ней пара. Расширение происходит при высокой температуре и сопровождается испарением воды; сжатие при низкой температуре сопровождается конденсацией пара. Количество испарившейся в цикле воды после завершения кругового процесса, очевидно, совпадает с количеством сконденсированного пара. Известно, что удельная теплота парообразования с ростом температуры уменьшается. Поэтому тепло, выделяемое при конденсации пара, больше, чем тепло, поглощаемое при испарении воды. За счет чего обеспечивается положительная работа в цикле?

Рис. 13 

5.5. Найти отношение выделенного тепла к поглощенному в обратимом цикле, изображенном на рис. 13. Поглощение тепла происходит в изотермическом процессе $\it 1 \to \it 2$ при температуре $T_1$, выделение - в изотермических процессах $\it 3 \to \it 4$, $\it 5 \to \it 6$ и $\it 7 \to \it 8$ при температурах, соответственно, $T_2$, $T_3$ и $T_4\;\;$ ( $T_2<T_3<T_4<T_1$). Участки переходов между изотермами - адиабатические. Известно, что на каждой из трех стадий изотермического сжатия выделяются одинаковые порции тепла.

Далее: 6.  Первое и второе Вверх: 5.  Второе начало термодинамики Назад: 5.3.  Принцип энтропии