Далее: 5.4.  Второе начало термодинамики Вверх: 5.  Второе начало термодинамики Назад: 5.2.  Постулат Клаузиуса и

5.3.  Принцип энтропии

Рассмотрим величину, приращение которой равно отношению тепла, поглощенного на участке обратимого процесса, к абсолютной температуре:

$$\Delta S\ =\ {\Delta Q\over T}\;.$$ (12)

При этом, очевидно, участок, на котором вычисляется величина $\Delta S$ , должен быть либо достаточно мал, чтобы изменением температуры на нем можно было пренебречь, либо он должен быть изотермическим (адиабатические участки из рассмотрения выбрасываются, так как для них $\Delta Q = 0\,$).

Сумма всех приращений $\Delta S$ в обратимом цикле Карно равна нулю. Действительно, на участке изотермического расширения при температуре $T_1$

$$\Delta S_{12}\ =\ \sum_1^2 \Delta S_i\ =\ \sum_1^2 {\Delta Q_... ... =\ {1\over T_1}\ \sum_1^2 \Delta Q_i\ =\ {Q_1\over T_1}\;\;\;,$$

на участке изотермического сжатия при температуре $T_2$

$$\Delta S_{34}\ =\ \sum_3^4 \Delta S_i\ =\ \sum_3^4 {\Delta Q_... ... {1\over T_2}\ \sum_3^4 \Delta Q_i\ =\ -\ {Q_2\over T_2}\;\;\;,$$

на адиабатических участках $\it 2 \to \it 3$ и $\it 4 \to \it 1\;\;\ \Delta S =\$0. Тогда в сумме за цикл, согласно (4), получаем:

$$\Delta S\ =\ \Delta S_{12}\ +\ \Delta S_{34}\ =\ {Q_1\over T_1}\ -\ {Q_2\over T_2}\ =\ 0\;\;.$$

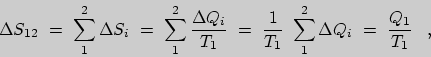
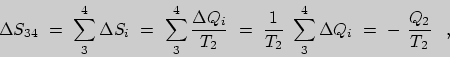
Обратим внимание, что полученный результат справедлив независимо от вещества рабочего тела, с которым осуществляется цикл Карно.

Рассмотрим цикл, состоящий из трех изотермических и трех адиабатических участков (см. рис. 9). На участке $\it 1 \to \it 2$ при температуре $T_1$ поглощается тепло $Q_1$, на участке $\it 3 \to \it 4$ при температуре $T_2$ выделяется тепло $Q_2$, на участке $\it 5 \to \it 6$ при температуре $T_3$ ($T_2<T_3<T_1$) выделяется тепло $Q_3$, участки $\it 2 \to \it 3$, $\it 4 \to \it 5$ и $\it 6 \to \it 1$ - адиабатические. Процессы изображены на диаграмме так, как они выглядели бы для идеального газа, однако здесь имеется в виду, что цикл может осуществляться с произвольным рабочим телом.

Рис. 9 

Найдем суммарное приращение $\Delta S$ в таком цикле. Мысленно продолжим адиабату $\it 4 \to \it 5$ до пересечения с изотермой $\it 1 \to \it 2$. Заменим прохождение рассматриваемого цикла последовательным прохождением двух циклов Карно: $\it 1 \to \it 2^\prime \to \it 5 \to \it 6 \to \it 1$ и $\it 2^\prime \to \it 2 \to \it 3 \to \it 4 \to \it 2^\prime$. При этом все изменения в системе будут, очевидно, такими же, как в цикле $\it 1 \to \it 2 \to \it 3 \to \it 4 \to \it 5 \to \it 6 \to \it 1$, поскольку при осуществлении двух циклов Карно все участки интересующего нас цикла будут пройдены по одному разу в нужных направлениях, а участок $\it 2^\prime \to \it 5$ проводится два раза в противоположных направлениях. Это означает, что суммарное приращение $\Delta S$ в исследуемом цикле равно нулю. Действительно, для циклов Карно имеем

$${Q_{12^\prime}\over T_1}\ =\ {Q_3\over T_3}\;;\;\;\; {Q_{2^\p... ...\over T_2}\;;\;\;\; (Q_1 = Q_{12^\prime} + Q_{2^\prime 2})\;\;.$$

Тогда изменение $S$ в цикле

$$\Delta S\ =\ {Q_{12^\prime}\over T_1}\ +\ {Q_{2^\prime 2}\over T_1}\ -\ {Q_2\over T_2}\ -\ {Q_3\over T_3}\ =\ 0\;\;.$$

Рассмотрим теперь произвольный обратимый цикл и заменим его на последовательное прохождение множества циклов Карно с малыми изотермическими участками (см. рис. 10). В пределе, когда протяженности изотермических участков неограниченно убывают, результат последовательности циклов Карно все более точно приближается к результату исследуемого цикла.

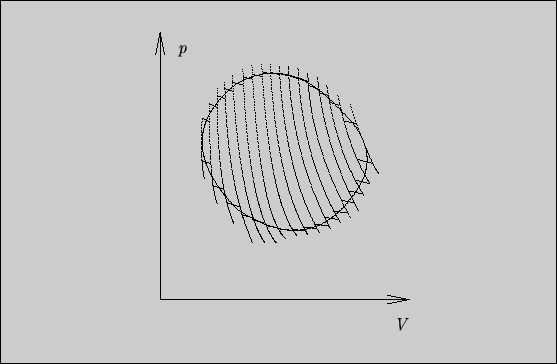
Рис. 10 

Действительно, отрезки адиабат, являющиеся общими для двух соседних циклов Карно, компенсируются за счет прямого и обратного прохождения (как в предыдущем примере), а изотермические участки и примыкающие к ним нескомпенсированные малые адиабатические отрезки приближаются к процессам в исследуемом цикле. Таким образом, если мы будем вычислять изменение величины $S$ в цикле, то мы должны просуммировать ее изменения во всех циклах Карно. Это дает основание обобщить результат, полученный ранее для цикла Карно и цикла, эквивалентного двум циклам Карно: сумма приращений

$$\Delta S\ =\ {\Delta Q\over T}$$

в любом обратимом цикле равна нулю.

Величина $S$ является, таким образом, функцией состояния (ее значения в начале и в конце любого кругового процесса одинаковы). Клаузиус назвал ее энтропией системы. Утверждение о том, что энтропия является функцией состояния, как мы убедились, представляет собой прямое следствие постулата Клаузиуса и может рассматриваться как одна из формулировок второго начала термодинамики для обратимых процессов (принцип энтропии). Иными словами, мы могли бы с самого начала принять в качестве постулата то, что функция, определенная через свое приращение соотношением (12), является функцией состояния, и на основе этого доказать принцип Клаузиуса.

Энтропия измеряется в единицах Дж/град. Как и внутренняя энергия, она обладает свойством аддитивности. Действительно, если равновесную систему разбить на части, то все они будут иметь одинаковую температуру, а тепло, поглощенное системой, будет складываться из порций тепла, поглощенных ее частями, поэтому изменение энтропии системы складывается из ее изменений для отдельных частей:

$$\Delta S_1+\Delta S_2+\ldots\ =\ {1\over T}\,(\Delta Q_1+\Delta Q_2+\ldots) \ =\ {\Delta Q\over T}\ =\ \Delta S\;.$$

Поскольку энтропия определена через ее приращение, само значение функции $S$ в конкретном состоянии задано с точностью до произвольного постоянного слагаемого, что в большинстве задач термодинамики оказывается достаточным.

Заметим, что в определении энтропии существенную роль играет обратимость процесса ее изменения. Это означает, что данное определение может использоваться лишь для равновесных состояний. Обобщить его на случай неравновесных состояний можно, пользуясь свойством аддитивности энтропии. При этом нужно мысленно разбить неравновесную систему на равновесные части (в большинстве случаев это возможно) и просуммировать значения их энтропий. Этот же подход можно использовать в задачах, где присутствует обмен веществом между системами.

Микроскопическое определение энтропии в молекулярной (статистической) физике, данное Больцманом, связано с понятием вероятности. При этом энтропия может быть охарактеризована как мера хаоса, беспорядка в системе, то есть чем менее упорядочено состояние системы (при данных значениях внутренней энергии и внешних сил), тем больше ее энтропия.

Далее: 5.4.  Второе начало термодинамики Вверх: 5.  Второе начало термодинамики Назад: 5.2.  Постулат Клаузиуса и