Далее: §18. Непрерывные случайные величины Вверх: Глава III. Случайные величины Назад: §16. Случайные величины и

§17. Закон больших чисел

Основными понятиями теории вероятностей являются понятия случайного события и случайной величины. При этом предсказать заранее результат испытания, в котором может появиться или не появиться то или иное событие или какое-либо определенное значение случайной величины, невозможно, так как исход испытания зависит от многих случайных причин, не поддающихся учету.

Однако при неоднократном повторении испытаний наблюдаются закономерности, свойственные массовым случайным явлениям. Эти закономерности обладают свойством устойчивости. Суть этого свойства состоит в том, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате большой массы подобных явлений, а характеристики случайных событий и случайных величин, наблюдаемых в испытаниях, при неограниченном увеличении числа испытаний становятся практически не случайными.

Пусть производится большая серия однотипных опытов. Исход каждого отдельного опыта является случайным, неопределенным. Однако, несмотря на это, средний результат всей серии опытов утрачивает случайный характер, становится закономерным.

Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел.

Под законом больших чисел не следует понимать какой-то один общий закон, связанный с большими числами. Закон больших чисел - это обобщенное название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным.

К ним относятся теоремы Чебышева и Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли - простейшим.

В основе доказательства теорем, объединенных термином "закон больших чисел", лежит неравенство Чебышева, по которому устанавливается вероятность отклонения $X$ от ее математического ожидания:

$$P\{\left\vert {X - M[X]} \right\vert < \xi \} \ge 1 - {\displaystyle D[X]\over\displaystyle \xi ^2}.$$

Пример 81. Устройство состоит из 100 независимо работающих элементов. Вероятность отказа каждого элемента за время $T$ равна 0,03. Оценить вероятность того, что абсолютная величина разности между числом (математическом ожиданием) отказов за время $T$ окажется: а) меньше двух; б) не меньше двух.

Решение. а). Обозначим через $X$ число отказавших элементов за время $T$. Тогда $M$[$X$] = np = 100 ? 0,03 = 3 и $D$[$X$] = npq = 100 ? 0,03 ? 0,97 = 2,91 (см. пример ). Воспользуемся неравенством Чебышева:

$$P\{\left\vert {X - M[X]} \right\vert < \xi \} \ge 1 - {\displaystyle D[X]\over\displaystyle \xi ^2},$$

подставив в него $M$[$X$] = 3, $D$[$X$] = 2,91, $\xi$ = 2, получим

$$P\{\left\vert {X - 3} \right\vert < 2\} \ge 1 - {\displaystyle 2,91\over\displaystyle 4} \approx 0,27.$$

б). События $\left\vert {X - 3} \right\vert < 2$ и $\left\vert {X - 3} \right\vert \ge 2$ противоположны, поэтому сумма их вероятностей равна единице. Следовательно,

$$P\{\left\vert {X - 3} \right\vert \ge 2\} \le 1 - 0,27 = 0,83.$$

Пример 82. Оценить вероятность события $\vert X$ - $M$[$X$]$\vert$< 3$\sigma$, где $\sigma$ - среднее квадратичное отклонение случайной величины $X$.

Решение. Полагая $\varepsilon$ = 3$\sigma$, получим в правой части неравенства число $1 - {\displaystyle D[X]\over\displaystyle 9\sigma ^2},{\rm т.е. }{\displaystyle {\rm 8}\over\displaystyle {\rm 9}}.$ Таким образом, вероятность события $M[X] - 3\sigma < X < M[X] + 3\sigma$ не меньше, чем ${\displaystyle 8\over\displaystyle 9}.$

В действительности для подавляющего большинства встречающихся на практике случайных величин эта вероятность значительно ближе к единице, чем ${\displaystyle 8\over\displaystyle 9}.$

В теореме Чебышева (справедлива как для дискретных, так и для непрерывных случайных величин) утверждается, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Формулируя теорему Чебышева, мы предполагали, что случайные величины имеют различные математические ожидания. На практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. Очевидно, что если вновь допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева.

Пример 83. Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. При каких условиях этот способ измерения можно считать правильным?

Решение. Ответ на этот вопрос даст теорема Чебышева (ее частный случай). Рассмотрим результаты каждого измерения как случайные величины X$_{1}$, X$_{2}$, ...X$_{n }$. К этим величинам можно применить теорему Чебышева, если: 1) они попарно независимы; 2) имеют одно и то же математическое ожидание; 3) дисперсии их ограничены.

Первое требование выполняется, если результат каждого измерения не зависит от результатов остальных. Второе требование выполняется, если измерения проведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру $а$. Третье требование выполняется, если прибор обеспечивает определенную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их ограничено. Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом $n$ вероятность неравенства

$$\left\vert {{\displaystyle X_1 + X_2 + ... + X_n \over\displaystyle n} - a} \right\vert < \varepsilon$$

как угодно близка к единице. Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отличается от истинного значения измеряемой величины.

Итак, теорема Чебышева указывает условия, при которых описанный способ измерения может быть применен. Однако, ошибочно думать, что увеличивая число измерений, можно достичь сколь угодно большой точности. Дело в том, что сам прибор дает показания лишь с точностью $\pm$$\alpha$; поэтому каждый из результатов измерений, а следовательно, и их среднее арифметическое будут получены лишь с точностью, не превышающей точности прибора.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят обо всей совокупности (генеральной совокупности) исследуемых объектов.

Пусть производится $n$ независимых испытаний, в каждом из которых вероятность появления события $A$ равна $р$. Можно ли предвидеть, какова примерно будет относительная частота появлений события? Положительный ответ на этот вопрос дает теорема, доказанная Якобом Бернулли (опубликована в 1713 г.), которая получила название "закона больших чисел" и положила начало теории вероятностей как науке. Доказательство Бернулли было сложным; простое доказательство дано П.Л. Чебышевым в 1846 г.

Теорема Бернулли. Если в каждом из $n$независимых испытаний вероятность $р$ появления события $A$ постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности $р$ по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Другими словами, если $\varepsilon$ сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство

$$\mathop {\lim }\limits_{n \to \infty } P\left( {\left\vert {... ...\displaystyle n} - p} \right\vert < \varepsilon } \right) = 1.$$

При доказательстве теоремы Бернулли получаем оценку

$$P\left\{ {\left\vert {{\displaystyle m\over\displaystyle n} ... ... \ge 1 - {\displaystyle pq\over\displaystyle n\varepsilon ^2}.$$

Как видим, теорема Бернулли объясняет, почему относительная частота при достаточно большом числе испытаний обладает свойством устойчивости и оправдывает статистическое определение вероятности (см. §12)

Пример 84. Оценим вероятность того, что при подбрасывании игральной кости 300 раз относительная частота появления шести очков отклонится от вероятности этого события не более чем на 0,01.

Решение. Для оценки события $\left\{ {\left\vert {{\displaystyle m\over\displaystyle n} - {\displaystyle 1\over\displaystyle 6}} \right\vert \le 0.01} \right\}$ применим неравенство из доказательства теоремы Бернулли, где $n = 300,p = {\displaystyle 1\over\displaystyle 6},q = {\displaystyle 5\over\displaystyle 6},\varepsilon = 0,05:$

$$P\left\{ {\left\vert {{\displaystyle m\over\displaystyle n} ... ...ystyle 6}\over\displaystyle 300 \cdot (0,05)^2} \approx 0,815.$$

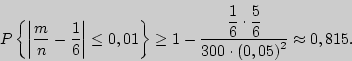
Пример 85. Вероятность того, что деталь не прошла проверку ОТК, равна 0,1. Найти вероятность того, что среди 200 случайно отобранных деталей окажется непроверенных от 10 до 30 деталей.

Решение. Воспользуемся неравенством Чебышева, определив $M$[$X$] и $\varepsilon$.

$M$[$X$] = np = 200$\cdot$0,1 = 20 и $\left\vert {X - 20} \right\vert \le \varepsilon ,\varepsilon - 20 \le X \le 20 + \varepsilon ,$ откуда $\varepsilon$ = 10. Следовательно,

$$P\left\{ {\left\vert {X - 20} \right\vert \le 10} \right\} \... ...ystyle 200 \cdot 0,1 \cdot 0,9\over\displaystyle 10^2} = 0,82.$$

Вопросы для самоконтроля

Приведите геометрическую иллюстрацию неравенства Чебышева.

В чем смысл теоремы Чебышева?

Использование интегральной теоремы Муавра-Лапласа для доказательства теоремы Бернулли.

Как вы понимаете сходимость по вероятности?

Теорема Пуассона и ее применение в теории измерений.

Что вы понимаете под законом больших чисел?

Обобщение теоремы Чебышева.

Проведите эксперимент для иллюстрации закона больших чисел.

Задачи

I 161. Оцените вероятность того, что $\vert X$ - $M$[$X$]$\vert$< 0,2, если $D$[$X$] = 0,01.

162. Дано $P${$\vert X$ - $M$[$X$]$\vert$< $\varepsilon$} $\ge$ 0,8 и $D$[$X$] = 0,004. Используя неравенство Чебышева, оценить $\varepsilon$ снизу.

163. В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время $T$ лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом включенных ламп и средним числом включенных ламп за время $T$ окажется: а) меньше трех; б) не меньше трех.

164. Используя неравенство Чебышева, оценить вероятность того, что

$\vert X$ - $M$[$X$]$\vert$< 0,1, если $D$[$X$] = 0,001.

165. Изготовлена партия деталей. Среднее значение длины детали равно 30 см, а среднее квадратическое отклонение равно 0,2 см. Оцените снизу вероятность того, что длина наудачу взятой детали окажется не менее 29,5 см и не более 30,5 см.

166. Дисперсия каждой из 1000 независимых случайных величин равна 4. Оцените вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий по абсолютной величине не превысит 0,2.

II 167. Применима ли к последовательности независимых случайных величин $X_{1 }$, $X_{2}$, ..., $X_{п}$, ... теорема Чебышева, если каждая случайная величина $X_{k}$ задана законом распределения

$X_{k}$	- k$\alpha$	0	k$\alpha$
P	${\displaystyle 1\over\displaystyle 2k^2}$	$1 - {\displaystyle 1\over\displaystyle k^2}$	${\displaystyle 1\over\displaystyle 2k^2}$

где постоянная величина $\alpha$ > 0?

168. Каждая из 1000 независимых случайных величин имеет дисперсию, равную 4, а математические ожидания их одинаковы. Оцените вероятность того, что среднее арифметическое случайных величин отклонится от математического ожидания по абсолютной величине не более чем на 0,1.

III 169. Применима ли к последовательности случайных величин $X_{1 }$, $X_{2}$, ..., $X_{п}$, ..., имеющих равномерное распределение в промежутке ]$a, b$[, теорема Чебышева?

170. Пусть $f(x)$ > 0 - неубывающая функция. Доказать, что если существует $M$[$f$ ($\vert X - M$[$X$]$\vert )$], то

$$P\left\{ {\left\vert {X - M[X]} \right\vert \ge \varepsilon ... ...ght\vert} \right)} \right]\over\displaystyle f(\varepsilon )}.$$

Далее: §18. Непрерывные случайные величины Вверх: Глава III. Случайные величины Назад: §16. Случайные величины и