Понятие совместного распределения переносится также на системы из более чем
двух с.в. В качестве мер связи используются коэффициенты парной корреляции,
которые удобно интерпретировать на графе. Корреляционным графом назовем
множество вершин, обозначающих переменные и соединенных попарно ребрами с
проставленными рядом соответствующими им коэффициентами корреляции. Так, для
трех случайных величин ![]() ,
, ![]() ,
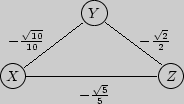
, ![]() корреляционный граф выглядит следующим образом:
корреляционный граф выглядит следующим образом:
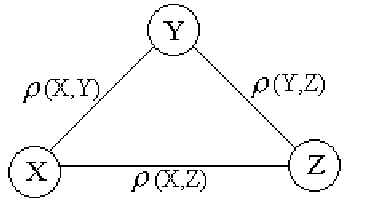
Пример 106. Найти корреляционный граф для числа белых, черных и красных шаров, оказавшихся в выборке из примера 103.
Решение. Приняв за с.в. ![]() = {число красных шаров в выборке}, находим
= {число красных шаров в выборке}, находим
![]() (
(![]() по ковариационному графу:
по ковариационному графу:
![]()
Тогда 2
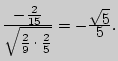
Аналогично находим коэффициент корреляции
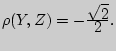
Следовательно, искомый корреляционный граф выглядит следующим образом:
Пример 107. Пусть ![]() - соответственно число выпадений "герба",
число серий "гербов" и длина максимальной из этих серий при трех бросаниях
монеты. Постройте корреляционный граф с.в.
- соответственно число выпадений "герба",
число серий "гербов" и длина максимальной из этих серий при трех бросаниях
монеты. Постройте корреляционный граф с.в. ![]() .
.
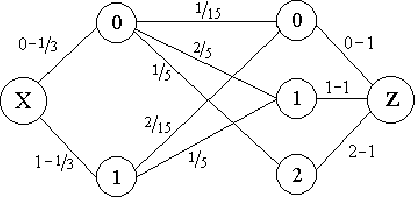
Решение. Используя вероятностное дерево для трех бросаний монеты, находим три ковариационных графа и по ним соответствующие коэффициенты корреляции.
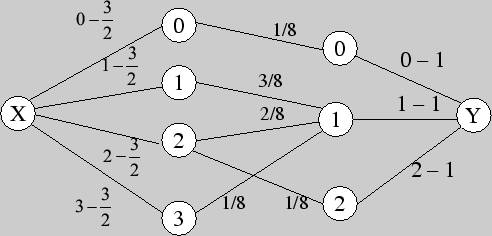
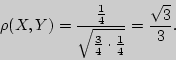
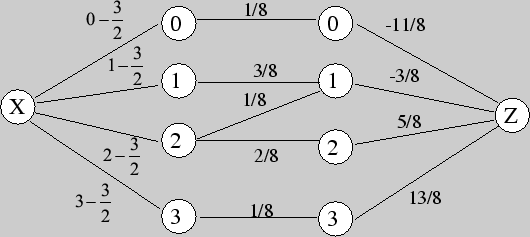
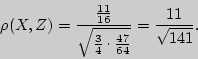
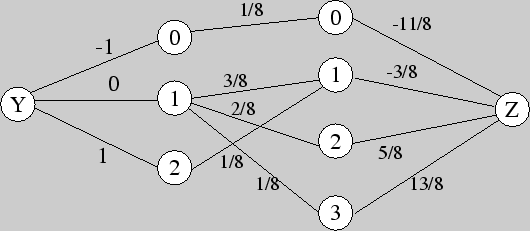
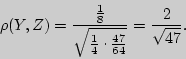
Следовательно, искомый корреляционный граф имеет вид
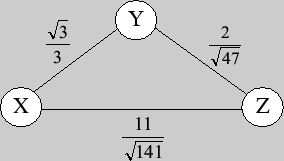
Пример 108. Доказать, что
![$D\left[ {x_1 + x_2 + ... + x_n
} \right] = \sum\limits_{i = 1}^n {\sigma _k ^2} +
2\sum\limits_{ij} {Cov(x_i ,x_j )} $](img1057.png) для случайных величин
для случайных величин
![]() ,
, ![]() , ...,
, ..., ![]() c конечными дисперсиями
c конечными дисперсиями
![]()
Решение.
Вычисляя математическое ожидание от обеих частей, получаем искомое соотношение.
Используем в дальнейшем полученный результат для выводов, которые прямыми вычислениями получаются достаточно сложно.
Пример 109. Найти математическое ожидание и дисперсию для числа совпадений занумерованных карт с номером раскладывания их в случайном порядке.
Решение. Определим с.в. ![]() , принимающую значения 1 или 0 в
зависимости от того, попала ли карта с номером
, принимающую значения 1 или 0 в
зависимости от того, попала ли карта с номером ![]() на
на ![]() -е место
или нет.
-е место
или нет.
Следовательно,
![]() и
и
![]() а
а
![$D\left[ {X_k } \right] = \sigma _k ^2 = M\left[
{X_k ^2} \right] - M^2\left[ {X...
...\over\displaystyle n}} \right)^2 = {\displaystyle n - 1\over\displaystyle n^2}.$](img1064.png)
Тогда
![$D\left[ {X_1 + X_2 + ... + X_n } \right] = n \cdot {\displaystyle n - 1\over\di...
...er\displaystyle n} + {\displaystyle n(n -
1)\over\displaystyle n^2(n - 1)} = 1.$](img1066.png) Таким образом, получили, что и математическое
ожидание, и дисперсия числа совпадений равны единице.
Таким образом, получили, что и математическое
ожидание, и дисперсия числа совпадений равны единице.
Пример 110. Найти дисперсию для гипергеометрического распределения (см. пример 73).
Решение. Введем с.в. ![]() , принимающую два значения 1 или 0 в зависимости
от того, является ли
, принимающую два значения 1 или 0 в зависимости
от того, является ли ![]() -й элемент в выборке белым или нет (l
-й элемент в выборке белым или нет (l ![]() k).
k).
a
![]() и
и
Следовательно,
Вопросы для самоконтроля
1. Какая случайная величина называется многомерной?
2. Приведите примеры трехмерной случайной величины.
3. Как можно рассматривать многомерную случайную величину?
4. Как можно описать степень связи составляющих многомерной случайной величины?
5. Что называется корреляционным графом?
6. Приведите примеры возможного корреляционного графа.
7. Какие существуют ограничения для корреляционного графа?
8. О чем можно судить по корреляционному графу?
Задачи
I 211. Составить законы распределения двух шаров, случайно размещающихся в трех ящиках.
212. Подбрасываем по одному разу игральную кость и монету. Построить графы распределения для числа выпадения шести очков, четного числа очков на игральной кости и числа выпадения "гербов" на монете.
213. Составить законы распределения для числа выпадения шести очков, числа очков, кратных трем, и четного числа очков при двух подбрасываниях игральной кости.
214. Подбрасываем один раз игральную кость и два раза монету. Построить ковариационные графы для числа выпадения шести очков, четного числа очков на игральной кости и числа выпадения "гербов" на монете.
215. Построить корреляционный граф для количества "дуплей", количества "костей" с суммой очков, равных 4 или 8, при случайном выборе одной "кости" из полного набора домино.
216. Построить корреляционный граф для количества "костей" с суммой в 12 очков, с четной суммой и с суммой очков, кратных трем при случайном выборе одной "кости" из полного набора домино.
II 217. Найти корреляционный граф для распределения трех шаров, случайно размещающихся в трех ящиках.
218. Из урны, содержащей один белый, три черных и пять красных шаров, последовательно извлекаем два шара. Найти корреляционный граф для числа белых, черных или красных шаров, оказавшихся в выборке.
III 219. В каком случае дисперсия суммы ![]() взаимно независимых
случайных величин, принимающих два значения 0 и 1, наибольшая?
взаимно независимых
случайных величин, принимающих два значения 0 и 1, наибольшая?
220. Построить корреляционный граф для числа выпаданий "герба", числа серий "гербов" и длины, максимальной из этих серий, при четырех подбрасываниях монеты.