Далее: §33. Выборочные характеристики вариационного Вверх: Глава V. Математическая статистика Назад: Глава V. Математическая статистика

§32. Вариационный и статистический ряд

В математической статистике исследуются утверждения, которые могут быть сделаны на основе измерения некоторой величины, на простейшем примере поясним постановку (одной из многих) задач математической статистики.

Пусть требуется измерить некоторую величину $a$. Результаты измерений

$$х_{1}, х_{2}, \ldots x_{n}$$

естественно рассматривать как значения случайных величин $Х_{1}, Х_{2}, \ldots , Х_{n}$, полученных в данном эксперименте. Если измерительный инструмент не имеет систематической ошибки, то можно положить $M[X_{n}] = a$. Следовательно, возникает задача оценить параметр $a$. Для решения задачи рассмотрим случайную величину

$$Х = {\displaystyle 1\over\displaystyle п}\sum\limits_{k = 1}^n {X_k } .$$

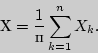
Тогда $M[Х] = M\left[ {{\displaystyle 1\over\displaystyle n}\sum\limits_{k = 1}^n {X_k } } \right] = a = M[X_k ].$

Это обстоятельство приводит к мысли построить статистические характеристики:

$$a^\ast \equiv \bar {a} = {\displaystyle 1\over\displaystyle n}\sum\limits_{i = 1}^n {x_i } ,$$

$$D^\ast \equiv \bar {D} = {\displaystyle 1\over\displaystyle n}\sum\limits_{i = 1}^n {(x_i - a)^2} .$$

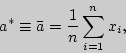
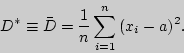
Первая представляет среднее арифметическое наблюденных значений случайной величины $X_{k}$ и статистическую дисперсию - во втором случае. В соответствии с законом больших чисел эти среднеарифметические сходятся по вероятности соответственно к математическому ожиданию величины $Х$ и к дисперсии

$$D[X] = M[(X - a)^2]: \bar {a} \to a, \bar {D} \to D.$$

При ограниченности наблюдений эксперимента заменой $M[X]$ и $D[X]$ на $\bar {а}$ и $\bar {D}$ совершаем погрешность, а при небольшом числе наблюдений величины $\bar {а}$ , $\bar {D}$ являются случайными величинами. Возникает задача об оценке неизвестных параметров $a$, $D$ случайной величины $X$ на основе экспериментальных данных, т.е. задача - найти подходящие значения этих параметров.

Множество результатов измерений $\{x_{1}, x_{2}, \ldots , x_{n}\}$ величины $Х$ называется выборкой объема $n$. Для того, чтобы иметь возможность воспользоваться аппаратом теории вероятностей, целесообразно наблюдаемую величину $Х$ рассматривать как случайную величину, функцию распределения которой

$$F(x)=P\{ X < x \}$$

следует определить.

Полученный статистический материал $х_{1}$, $х_{2}$, ...$x_{n}$ наблюдений представляет собой первичные данные о величине, подлежащей статистической обработке. Обычно такие статистические данные оформляются в виде таблицы, графика, гистограммы и т.д.

Если выборка объема $n$ содержит $k$ различных элементов $x_{1}', x_{2}', \ldots , x_{k}'$, причем $x_{i}'$ встречается $m_{i}$ раз, то число $m_{i}$ называется частотой элемента $x_{i}'$, а отношение ${\displaystyle m_i\over\displaystyle n} = f_i$ называется относительной частотой элемента $x_{i}'$. Очевидно, что $\sum\limits_{i = 1}^n {f_i } = 1.$

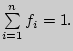
Вариационным (статистическим) рядом называется таблица, первая строка которой содержит в порядке возрастания элементы $x_{i}$', а вторая - их частоты $m_{i}$ (относительные частоты $f_{i })$.

Полигоном частот (относительных частот) выборки называется ломаная с вершинами в точках ($x_{i}$, $m_{i})$ ( ($x_{i}$, $f_{i })$ ).

Функция $F_{n}(x)=l/n$, где $n$ - объем выборки, а $l$ - число значений $X$ в выборке, меньших $x$, называется эмпирической функцией распределения. Функция $F_{n}(x)$ служит оценкой неизвестной функции распределения $F(x)$, т.е. $F_{n}(x) \to F(x)$.

Пусть теперь $Х$ - непрерывная случайная величина с неизвестной плотностью вероятности $f(x)$. Для оценки $f(x)$ по выборке $х_{1}, х_{2}, \ldots x_{n}$ разобьем область значений $Х$ на интервалы длины $h_{i} (i = 1, 2, \ldots , s)$. Обозначим через $\tilde {х}_i$ середины интервалов, а через $m_{i}$ число элементов выборки, попавших в указанный интервал. Тогда $f(\tilde {x}_i )\sim {\displaystyle m_i \over\displaystyle nh_i }$ - оценка плотности вероятности в точке $\tilde {х}_i$. В прямоугольной системе координат построим прямоугольники с основаниями $h_{i}$ и высотами ${\displaystyle m_i \over\displaystyle nh_i}$, т.е. площади прямоугольника, равной относительной частоте данного разряда. Полученная таким образом фигура называется гистограммой выборки.

Пример 156. Имеются данные о количестве студентов в 30 группах физико-математического факультета:

26	25	25	26	25	23
23	24	19	23	20	19
22	24	24	23	20	23
24	19	21	18	21	18
20	18	18	21	15	15

Найти вариационный ряд количества студентов в группах и размах варьирования. Построить полигон частот.

Решение. Записывая исходные данные в порядке возрастания, составим вариационный ряд:

$x_{i}$	15	18	19	20	21	22	23	24	25	26
$m_{i}$	2	4	2	4	3	1	5	4	3	2

Размах варьирования $R = x_{max} - x_{min} = 26 - 15 = 11$.

Для построения полигона частот обозначим на оси абсцисс возможные значения признака, а на оси ординат соответствующие частоты $m_{i}$ и полученные точки соединим отрезками.

Рис. 96

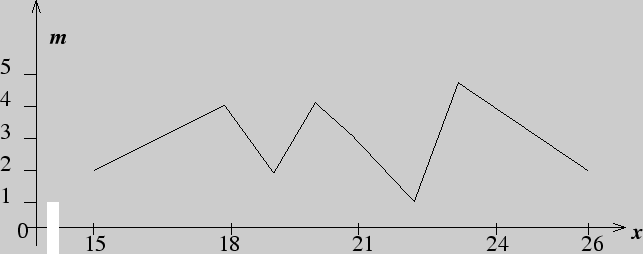
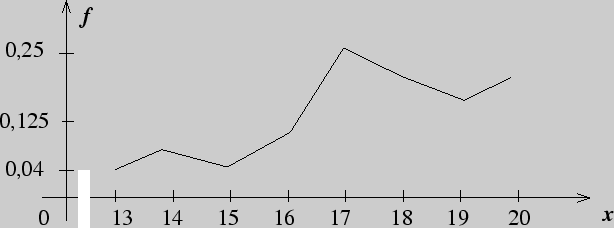
Пример 157. Школьникам предлагалось разгадать несколько числовых закономерностей и вписать в пропуски недостающие числа. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:

Кол-во баллов	13	14	15	16	17	18	19	20
Кол-во школьников	2	3	2	4	12	10	8	9

Составить статистическое распределение количества школьников по количеству набранных баллов и построить полигон относительных частот.

Решение. Пусть $X$ = {количество набранных баллов}, a $f$ = {относительные частоты}. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:

X	13	14	15	16	17	18	19	20
$f$	0,04	0,06	0,04	0,08	0,24	0,2	0,16	0,18

Чтобы построить полигон относительных частот, отложим на оси абсцисс значения $Х$, а на оси ординат - относительные частоты $f$. После этого последовательно соединим полученные точки отрезками.

Рис. 97

Пример 158. В 2002 году количество служб, представляющих гражданам жилищные субсидии, по сельским районам области распределено следующим образом:

5, 1, 1, 1, 1, 1, 5, 1, 10, 1, 1, 1, 4, 4, 5, 1, 1.

Построить эмпирическую функцию распределения.

Решение. Найдем сначала статистический ряд распределения числа служб в районах области.

$x_{i}$	1	4	5	10
$f_{i}$	${{11} \over {17}}$	${2 \over {17}}$	${3 \over {17}}$	${1 \over {17}}$

Эмпирическую функцию распределения находим аналогично интегральной функции (см. §13) [перейти].

$F_{17} (x) = \left\{ {\begin{array}{l} 0{\rm , если }х \le 1, [5pt] {\disp... ..., если 5} < х \le 10, [5pt] 1{\rm , если }х > 10. \\ \end{array}} \right.$

Рис. 98

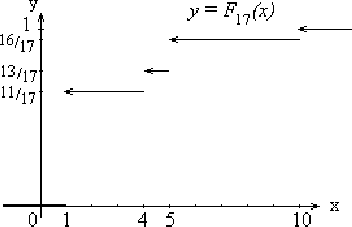
Пример 159. Построить гистограмму следующей выборки объема 50

Номер интервала	Границы интервала $x_{i} - x_{i + 1}$	Сумма частот вариант интервала $m_{i}$	Плотность относительной частоты $m_{i}/{ n \cdot h_i}$
1	3 - 7	5
2	7 - 12	10
3	12 - 17	20
4	17 - 21	8
5	21 - 28	7

Решение. Найдем плотность $m_{i}/{ n \cdot h_i}$ относительной частоты $m_{i}/{n}$ для каждого интервала и заполним последний столбец таблицы:

$$\raise0.7ex\hbox{${m_1 }$} \!\mathord{\left/ {\vphantom {{m_... ...\nulldelimiterspace}\!\lower0.7ex\hbox{${50 \cdot 7}$} = 0,02.$$

Построим на оси абсцисс заданные интервалы и проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся на расстояниях, равных соответствующим плотностям относительной частоты $m_{i}/{ n \cdot h_i}$.

Рис. 99

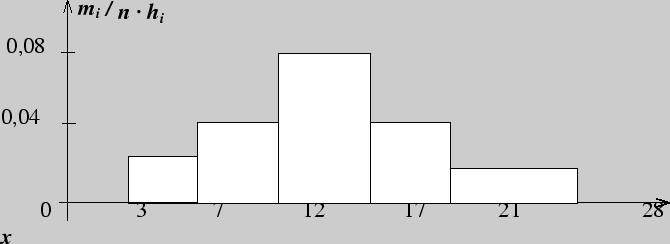
Из способа построения гистограммы следует, что полная ее площадь равна единице.

Пример 160. Число школ Ярославской области в 2002 - 2003 учебном году по малым городам и районам составило:

20, 21, 31, 17, 13, 21, 16, 17, 26, 19, 15, 20, 17, 22, 28, 29, 25.

Построить гистограмму распределения числа школ по районам области.

Решение. Выберем границы интервалов и составим по данной выборке следующую таблицу

Номер интервала	Границы интервала $x_{i} - x_{i + 1}$	Сумма частот вариант интервала $m_{i}$	Плотность относительной частоты $m_{i}/{ n \cdot h_i}$
1	13 - 17	6	${6 \over {17 \cdot 4}} = \textstyle{3 \over {34}}$
2	17 - 20	3	${3 \over {17 \cdot 3}} = \textstyle{1 \over {17}}$
3	20 - 25	4	${4 \over {17 \cdot 5}} = \textstyle{4 \over {85}}$
4	25 - 31	4	${4 \over {17 \cdot 6}} = \textstyle{2 \over {51}}$

Аналогично предыдущему примеру строим гистограмму числа школ, распределенных по малым городам и районам области.

Рис. 100

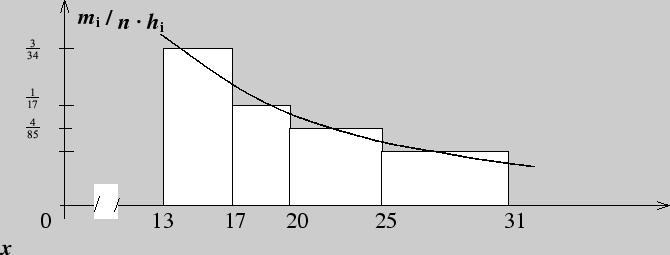
"Сглаживая" полученную гистограмму, получаем "похожесть" данного дискретного закона распределения на классический показательный (непрерывный) закон. В этом и заключается основное предназначение гистограмм выборок.

Вопросы для самоконтроля

На каких методах основано изучение статистических данных?

Основные задачи математической статистики.

Какие способы отбора из генеральной совокупности вы знаете?

Какая выборка называется представительной?

В чем отличие вариационного от статистического ряда?

Для чего используется полигон частот?

Свойства эмпирической функции распределения.

В каком случае и для чего строятся гистограммы?

Задачи

I. 311. Записать выборку 2, 7, 3, 5, 4, 10, 5, 5, 2, 8, 10, 2, 7, 7, 7, 5, 4, 2, 4, 7, 8 в виде: а) вариационного ряда; б) статистического ряда.

312. Найдите эмпирическую функцию распределения для выборки, представленной вариационным рядом:

$x_{i}$	1	2	4	7
$m_{i}$	10	20	30	40

313. Имеются данные о количестве сельских населенных пунктов районов Ярославской области с численностью населения более 500 человек:

Большесельский - 4, Борисоглебский - 2, Брейтовский - 1, Гаврилов-Ямский - 2, Даниловский - 2, Любимский - 1, Мышкинский - 0, Некоузский - 6, Некрасовский - 5, Первомайский - 2, Переславский - 11, Пошехонский - 0, Ростовский - 11, Рыбинский - 12, Тутаевский - 3, Угличский - 4, Ярославский - 27.

Найдите вариационный ряд количества населенных пунктов Ярославской области с численностью населения более 500 человек. Постройте полигон частот.

314. В 2002 году количество крупных и средних промышленных предприятий по районам ( в том же порядке, что и в предыдущей задаче) области распределено следующим образом:

2, 2, 2, 6, 5, 6, 1, 4, 1, 5, 4, 4, 9, 6, 3, 0, 6.

Постройте полигон частот и эмпирическую функцию распределения.

315. Количество учащихся, получивших аттестат с медалью, в 2001 году по городам и районам Ярославской области:

г. Ярославль - 280, г. Рыбинск - 66, г. Ростов - 61, г. Переславль - 27, г. Углич - 32, г. Тутаев - 36;

Большесельский - 8, Борисоглебский - 3, Брейтовский - 11, Гаврилов-Ямский - 7, Даниловский - 19, Любимский - 11, Мышкинский - 3, Некоузский - 15, Некрасовский - 7, Первомайский - 6, Переславский - 1, Пошехонский - 8, Ярославский - 30.

Найдите вариационный ряд распределения медалистов, размах варьирования и среднее число медалистов по городам и районам области.

316. Посевные площади картофеля (тыс. гектаров) в сельских хозяйствах Ярославской области по районам:

1,5; 1,5; 0,6; 1,3; 0,9; 0,9; 0,6; 1,3; 1,1; 0,6; 1,1; 0,9; 1,6; 1,3; 0,8; 0,4; 1,1.

Найдите статистический ряд распределения посевных площадей и постройте полигон относительных частот.

II. 317. Построить гистограмму выборки, представленной в виде таблицы частот. Объем выборки $n = 100$.

Номер интервала	Границы интервала $x_{i}$ - $x_{i + 1}$	Сумма частот вариант интервала $m_{i}$
1 2 3 4	1 - 5 5 - 8 8 - 13 13 - 15	24 30 40 6

318. Построить гистограмму выборки объема $n = 75$, представленной в виде таблицы частот:

Номер интервала	Границы интервала $x_{i}$ - $x_{i + 1}$	Сумма частот вариант интервала $m_{i}$
1 2 3 4 5 6	0 - 2 2 - 4 4 - 7 7 - 12 12 - 15 15 - 20	3 6 8 25 15 18

III. 319. Директорский корпус средних школ Ярославской области характеризуется по стажу работы следующим образом:

до 2-х лет - 6 человек, от 2 до 5 - 7, от 5 до 10 - 21 человек, от 10 до 20 - 59 человек, свыше 20 - 196, пенсионеров - 65 человек. Получите интервальный ряд распределения и постройте гистограмму относительных частот стажа директоров школ области.

320. Рождаемость (смертность) населения Ярославской области в 2003 году по малым городам и районам области составили:

85, 159, 80, 249, 289, 151, 105, 180, 199, 122, 153, 157, 336, 231, 148, 96, 519;

309, 350, 267, 738, 750, 371, 239, 598, 715, 277, 726, 466, 905, 777, 415, 376, 993.

Найдите интервальные ряды распределения и гистограммы рождаемости и смертности по районам Ярославской области.

Далее: §33. Выборочные характеристики вариационного Вверх: Глава V. Математическая статистика Назад: Глава V. Математическая статистика