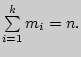
Пусть выборка задана вариационным рядом
| . . . | , где
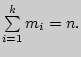 |
||||
| . . . |
Выборочным средним называется величина
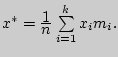
Выборочная дисперсия
![$D^\ast [X] = {\displaystyle 1\over\displaystyle n}\sum\limits_{i = 1}^k
{(x_i - x^\ast )^2 \cdot m_i } ,$](img1461.png) а корень квадратный из выборочной
дисперсии называется выборочным средним квадратическим отклонением
а корень квадратный из выборочной
дисперсии называется выборочным средним квадратическим отклонением
![]()
Выборочные начальные и центральные моменты порядка ![]() определяются
соответственно формулами:
определяются
соответственно формулами:
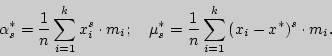
Модой ![]() называется вариант, наиболее часто
встречающийся в данном вариационном ряду.
называется вариант, наиболее часто
встречающийся в данном вариационном ряду.
Медианой ![]() называется вариант
называется вариант ![]() такой, что
такой, что
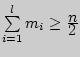 и
и
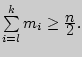 Медиана обладает тем свойством, что сумма абсолютных
величин отклонений вариантов от медианы меньше, чем от любой другой величины
(в том числе и от выборочной средней).
Медиана обладает тем свойством, что сумма абсолютных
величин отклонений вариантов от медианы меньше, чем от любой другой величины
(в том числе и от выборочной средней).
Важность эмпирических характеристик заключается в том, что они близки (при
достаточно большом ![]() ) к соответствующим теоретическим значениям. Поскольку
выборочные характеристики являются случайными величинами, а теоретические -
числа, то близость понимается в смысле сходимости по вероятностям.
) к соответствующим теоретическим значениям. Поскольку
выборочные характеристики являются случайными величинами, а теоретические -
числа, то близость понимается в смысле сходимости по вероятностям.
Пример 161. Известно распределение золотых медалистов, окончивших в 2001 году школы Ярославской области, по районам:
| Кол-во золотых медалистов | 0 | 1 | 3 | 4 | 6 | 8 | 20 |
| Кол-во районов | 6 | 1 | 4 | 2 | 1 | 3 | 1 |
Дайте характеристику распределения признака (число золотых медалистов по районам), вычислив для этого:
а) выборочную среднюю, б) моду и медиану, в) показатели вариации (дисперсию, среднее квадратическое отклонение, размах варьирования).
Решение. а)
![]()
б) ![]() , т.к.
, т.к.
![]() .
.
![]() , т.к.
, т.к.
![]() и
и
![]()
в)
![]()
![]() .
.
Пример 162. Измерение роста (в см) 100 студентов-первокурсников университета дало следующие результаты:
| Рост | 154-158 | 158-162 | 162-166 | 166-170 | 170-174 | 174-178 | 178-182 |
| Число студ-ов | 10 | 14 | 26 | 28 | 12 | 8 | 2 |
Найдите выборочную среднюю и выборочное среднее квадратическое отклонение роста первокурсников.
Решение. В качестве вариант ![]() примем середины интервалов и найдем
выборочную среднюю роста студентов.
примем середины интервалов и найдем
выборочную среднюю роста студентов.
![]() (см). Вычислим теперь
выборочную дисперсию
(см). Вычислим теперь
выборочную дисперсию
и, извлекая из полученного числа корень квадратный, находим среднее квадратическое отклонение
![]() (см).
(см).
Допустим, что все значения количественного признака ![]() разбиты на
разбиты на ![]() групп.
Рассматривая каждую группу как самостоятельную совокупность, можно найти
групповые средние и дисперсии. Внутригрупповой дисперсией
называют среднюю арифметическую дисперсий, взвешенную по объемам групп:
групп.
Рассматривая каждую группу как самостоятельную совокупность, можно найти
групповые средние и дисперсии. Внутригрупповой дисперсией
называют среднюю арифметическую дисперсий, взвешенную по объемам групп:
![]() - объем группы
- объем группы ![]() ,
,
![]() .
.
Межгрупповой дисперсией называют дисперсию групповых средних относительно общей средней:
![]() .
.
Пример 163. Найти групповые, внутригрупповую, межгрупповую и общую дисперсии совокупности, состоящей из следующих двух групп:
| Первая группа | Вторая группа | ||||||||
| 2 | 4 | 7 | 3 | 5 | 6 | 10 | |||
| 3 | 5 | 2 | 4 | 4 | 3 | 4 | |||
Решение. 1). Найдем общую и групповые средние:
и, используя их, - групповые дисперсии:
2). Найдем внутригрупповую и межгрупповую дисперсии
3). Найдем общую дисперсию
Для вычисления выборочных характеристик при больших выборках используют метод произведений, который продемонстрируем на следующем примере.
Пример 164. Найти выборочные среднюю и дисперсию следующего статистического распределения:
| 20,0 | 20,2 | 20,4 | 20,6 | 20,8 | 21,0 | 21,2 | 21,4 | 21,6 | 21,8 | 22,0 | |
| 2 | 3 | 7 | 11 | 17 | 20 | 16 | 13 | 6 | 4 | 1 |
Решение. Составим расчетную таблицу, для чего
Контроль:
![]() , и вычисления
произведены правильно.
, и вычисления
произведены правильно.
| 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
||||
| 20,0 | 2 | -5 | -10 | 50 | 32 |
| 20,2 | 3 | -4 | -12 | 48 | 27 |
| 20,4 | 7 | -3 | -21 | 63 | 28 |
| 20,6 | 11 | -2 | -22 | 44 | 11 |
| 20,8 | 17 | -1 | -17 | 17 | 0 |
| 21,0 | 20 | 0 | 20 | ||
| 21,2 | 160 | 1 | 16 | 16 | 64 |
| 21,4 | 13 | 2 | 26 | 52 | 117 |
| 21,6 | 6 | 3 | 18 | 54 | 96 |
| 21,8 | 4 | 4 | 16 | 64 | 100 |
| 22,0 | 1 | 5 | 5 | 25 | 36 |
| 100 | |||||
|
|
|
|
Вычислим теперь условные моменты первого и второго порядков:
Найдем искомые выборочные среднюю и дисперсию:
Если первоначальные варианты не являются равноотстоящими, то интервал, в котором заключены все варианты выборки, делят на несколько равных частичных интервалов.
Пример 165. Найти выборочную среднюю и выборочную дисперсию для следующего вариационного ряда:
| 1 | 1,03 | 1,05 | 1,06 | 1,08 | 1,10 | 1,12 | 1,13 | 1,16 | 1,19 | 1,20 | 1,21 | 1,25 | 1,26 | 1,28 | ||
| 1 | 3 | 6 | 4 | 2 | 4 | 3 | 6 | 5 | 2 | 4 | 4 | 8 | 4 | 4 | ||
| 1,30 | 1,32 | 1,35 | 1,37 | 1,38 | 1,39 | 1,40 | 1,44 | 1,46 | 1,47 | 1,49 | 1,50 | |||||
| 6 | 4 | 6 | 5 | 1 | 2 | 2 | 3 | 3 | 4 | 3 | 2 |
Решение. Выделим пять частичных интервалов:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим новый вариационный ряд из середин выбранных частичных интервалов:
| 1,05 | 1,15 | 1,25 | 1,35 | 1,45 | |
| 18 | 20 | 25 | 22 | 15 |
![]() и сравнивая с
и сравнивая с
![]() ,
замечаем, что
,
замечаем, что
![]() ,
а вычмслений значительно меньше.
,
а вычмслений значительно меньше.
Вопросы для самоконтроля
Задачи
I. 321. ![]() - частицы, достигающие счетчика в некотором
опыте, образуют следующую выборку:
- частицы, достигающие счетчика в некотором
опыте, образуют следующую выборку:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 21 | 81 | 156 | 200 | 195 | 152 | 97 | 54 | 26 | 11 | 7 |
Найдите выборочную среднюю, моду и медиану для числа ![]() - частиц,
достигающих счетчика.
- частиц,
достигающих счетчика.
322. Распределение рабочих цеха по проценту выполнения норм выработки выглядит следующим образом:
| % выполнения норм | 50 - 70 | 70 - 90 | 90 - 110 | 110 - 130 | 130 - 150 | 150 - 170 |
| Число рабочих | 20 | 25 | 35 | 30 | 20 | 10 |
Найдите средний процент выполнения норм выработки рабочими цеха.
323. Для определения "общего интеллекта" школьникам предлагалось раскрыть геометрические закономерности. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:
| Кол-во баллов | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Кол-во школьников | 4 | 11 | 15 | 16 | 19 | 15 | 5 |
Найдите моду и медиану данного вариационного ряда.
324. Дайте характеристику изменений показателей психологической защищенности младших подростков до и после эксперимента, в ходе которого получены следующие результаты:
| Показатели
психологической защищенности |
от публичного унижения | от оскорблений | от высмеиваний | от угроз | от обзываний | от непр. отношений | от игнорирования | от недобрых отношений |
| до эксперимента | 2,4 | 2,1 | 2,2 | 2,5 | 2,2 | 2,2 | 2,4 | 2,2 |
| после эксперимента | 2,6 | 2,2 | 2,4 | 2,8 | 2,3 | 2,6 | 2,8 | 2,4 |
325. Какой вывод можно сделать об эффективности интерактивного обучения по выраженности базовых ценностей и экологических ориентаций в экспериментальной и контрольной группах в конце обучения? Количества выборов представлены в таблице:
| Наименование показателя | Признание и уважение людей | Природа как среда сущ. любимых животных и растений |
Природа как условие благополучия будущего поколения | Природа как объект заботы |
| среднее по эксп. группе | 6,64 | 2,24 | 4,4 | 3,92 |
| среднее по контр. группе | 4,95 | 3,53 | 3,53 | 2,88 |
326. Найдите внутригрупповую, межгрупповую и общую дисперсию выборки, состоящей из трех групп:
первая группа
| 2 | 3 | 8 | |
| 30 | 20 | 10 |
вторая группа
| 1 | 6 | |
| 10 | 20 |
третья группа
| 3 | 5 | 7 | |
| 8 | 12 | 10 |
II. 327. Найдите методом произведений выборочную среднюю и выборочную дисперсию по заданному распределению выборки объема n = 100:
| варианты | 22 | 24 | 26 | 28 | 30 | 32 |
| частота | 5 | 15 | 50 | 18 | 10 | 4 |
328. Найдите методом произведений выборочные среднюю и дисперсию вариационного ряда:
| 6,2 | 6,4 | 6,6 | 6,8 | 7,0 | 7,2 | 7,4 | 7,6 | 7,8 | 8,0 | |
| 2 | 3 | 8 | 13 | 25 | 20 | 12 | 10 | 6 | 1 |
III. 329. Вычислите выборочные средние и дисперсии по первоначальным и равностоящим вариантам (и сравните их) для вариационного ряда:
| 1,00
1,03 1,05 1,06 1,08 1,10 |
1
3 6 4 2 4 |
1,12
1,15 1,16 1,19 1,20 1,23 |
3
6 5 2 4 4 |
1,25
1,26 1,29 1,30 1,32 1,33 |
8
4 4 6 4 5 |
330.Найдите выборочную среднюю и выборочную дисперсию по первоначальным и равностоящим вариантам для следующего вариационного ряда:
| 2 | 3 | 7 | 9 | 11 | 12,5 | 16 | 18,5 | 23 | 25 | 26 | |
| 3 | 5 | 10 | 6 | 10 | 4 | 12 | 13 | 8 | 20 | 9 |