Далее: Литература
Вверх: Дидактический модуль "Введение в
Назад: §3. Фрейм аннотированной учебной
Лабораторный практикум
| №
п/п |
№
раздела учеб. предм. |
Наименование лабораторной
работы |
| 1 |
1 |
1. Компьютерный контроль 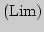 по теме "Предел
функции" (2 часа) по теме "Предел
функции" (2 часа)
2. Нахождение корней трансцендентных уравнений (графический
калькулятор) (2 часа) |
| 2 |
2 |
1. Компьютерный контроль 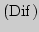 по теме "Производная"
(2 часа) по теме "Производная"
(2 часа)
2. Нахождение
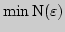 для числовой последовательности для числовой последовательности
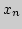 (педагогический программный продукт) (2 часа) (педагогический программный продукт) (2 часа)
3. Нахождение корней многочлена методом хорд (графический
калькулятор) (2 часа) |
Таблица 9
График учебного процесса
![\fbox{\footnotesize
\unitlength=1.00mm
\special{em:linewidth 0.4pt}
\linethickne...
...0){\makebox(0,0)[cc]{*}}
\put(139.00,64.00){\makebox(0,0)[cc]{*}}
\end{picture}}](img1552.png)
Рефераты (I семестр)
1. Построение графиков функций в полярной системе координат
- 1.
- Н.А.Вирченко, И.И.Ляшко, К.И.Швецов. Графики функций:
Справочник. Киев: Наук. думка, 1979.
- 2.
- Г.М.Фихтенгольц. Курс дифференциального и интегрального
исчисления. Т. 1. М.: Наука, 2001.
2. Десять исторических задач, приводящих к понятию
производной
- 1.
- А.П.Юшкевич. Концепции вычисления бесконечно малых
Ньютона и Лейбница // ИМИ. Вып. 23. 1978.
- 2.
- Д.Я. Стройк. Краткий очерк истории математики. М.: Мир,
1978.
3. Функциональные уравнения основных элементарных функций
- 1.
- Г.М.Фихтенгольц. Курс дифференциального и интегрального
исчисления. Т. 1. М.: Наука, 2001.
- 2.
- В.П.Одинец, А.И.Поволоцкий. Построение элементарных
функций. СПб.: Образование, 1995.
4. Основные элементарные функции в природе и технике
- 1.
- Н.Я.Виленкин. Функции в природе и технике. Книга для
внеклассного чтения IX-X классов. М.: Просвещение, 1978.
- 2.
- С.Г.Крейн, В.Н.Ушаков. Математический анализ
элементарных функций. М.: Наука, 1966.
- 3.
- Ф.Клейн. Элементарная математика с точки зрения высшей.
Т. 1. М.-Л., 1987.
5. Системы координат на плоскости и в пространстве
- 1.
- Л.С.Понтрягин. Метод координат. М.: Наука, 1977.
- 2.
- М.Я.Выготский. Справочник по высшей математике. М.:
Наука, 1973.
- 3.
- И.М.Гельфанд, Е.Г.Глаголева, А.А.Кириллов. Метод
координат. М., 1973.
6. Трансцендентные числа в анализе
- 1.
- В.А.Зорич. Математический анализ. Т. 1. М.: Наука,
1983.
- 2.
- Ф.Рудно. Квадратура круга. М.-Л., 1934.
- 3.
- А.О.Гельфонд. Решение уравнение в целых числах. М.-Л.,
1952.
- 4.
- А.Я.Хинчин. Три жемчужины теории чисел. М., 1979.
7. Цепные дроби и их приложения
- 1.
- А.Я. Хинчин. Цепные дроби. М.: Наука, 1978.
- 2.
- И.К.Андронов, А.К.Окунев. Арифметика рациональных
чисел. М.: Просвещение, 1971.
Контрольные вопросы и задания для самостоятельной работы
1. Доказать, что последовательность, задаваемая рекуррентным
соотношением: 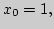
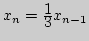 , сходится.
, сходится.
2. Найти пределы последовательностей:
а)
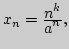
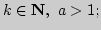
б)
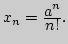
3. Будут ли следующие множества ограничены:
4. Будут ли семейства функций равномерно ограниченными:
5. Пусть 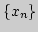 ограниченная последовательность. Следует ли
отсюда ее сходимость?
ограниченная последовательность. Следует ли
отсюда ее сходимость?
6. Пусть дано бесконечное число последовательностей:
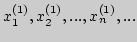 |
- I
последовательность, |
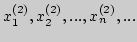 |
- II
последовательность, |
| ................ |
|
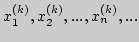 |
- 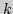 последовательность.
последовательность. |
Известно, что для любого 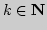 последовательность
последовательность
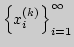 сходится к нулю и для
любого
сходится к нулю и для
любого 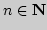 последовательность
последовательность
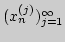 сходится к нулю. Что можно сказать о сходимости "диагональной"
последовательности
сходится к нулю. Что можно сказать о сходимости "диагональной"
последовательности
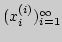 ?
?
7. Описать все замкнутые, выпуклые множества на прямой.
8. Пусть 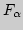 - произвольное семейство замкнутых, выпуклых
множеств на прямой. Доказать: если любые два множества семейства
- произвольное семейство замкнутых, выпуклых
множеств на прямой. Доказать: если любые два множества семейства
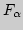 пересекаются по непустому множеству, то все множества
имеют общую точку.
пересекаются по непустому множеству, то все множества
имеют общую точку.
9. Найти точные нижние и верхние грани следующих множеств:
Пусть 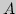 - некоторое подмножество метрического пространства
- некоторое подмножество метрического пространства
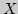 . Через
. Через 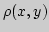 будем обозначать расстояние между
элементами
будем обозначать расстояние между
элементами 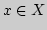 и
и 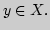 Наилучшим приближением элемента
Наилучшим приближением элемента
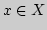 элементами множества
элементами множества 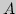 называется число
называется число
Элемент 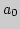 , на котором достигается точная нижняя грань,
называется элементом наилучшего приближения.
, на котором достигается точная нижняя грань,
называется элементом наилучшего приближения.
Геометрически наилучшее приближение элемента 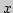 есть расстояние
от
есть расстояние
от 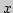 до множества
до множества 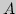 , а элемент наилучшего приближения -
точка
, а элемент наилучшего приближения -
точка 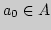 , ближайшая к
, ближайшая к 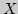 .
.
10. Пусть 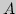 - множество рациональных чисел из
- множество рациональных чисел из ![$[0,1]$](img227.png) ,
, 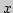 -
иррациональное число, принадлежащее этому отрезку. Найти
наилучшее приближение
-
иррациональное число, принадлежащее этому отрезку. Найти
наилучшее приближение 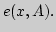
11. Докажите, что
а)
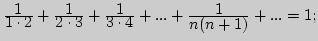
б)
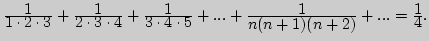
12. Найдите сумму ряда:
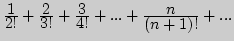
Примерный перечень вопросов к экзамену (интегративные учебные
элементы)
1. Мощность множества. Шкала мощностей (упорядочение,
неограниченность сверху, линейность). Счетные множества.
Несчетность континуума.
Построение шкалы мощностей с помощью факторизации по отношению
эквивалентности. Теорема Кантора-Бернштейна. Несчетность интервала
и всей прямой. Теорема Кантора о высших мощностях. Счетность
множества рациональных чисел. Мощности множеств 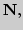
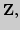
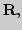
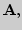
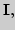
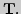
2. Аксиоматическое построение множества действительных чисел.
Три теории действительных чисел.
Основные группы аксиом: сложение, умножение, порядок, связи,
аксиома непрерывности. Лемма Кантора о вложенных отрезках.
Натуральные числа, метод математической индукции. Подклассы 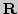 (натуральные
(натуральные 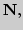 целые
целые 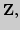 рациональные
рациональные 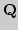 ,
иррациональные
,
иррациональные 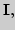 алгебраические
алгебраические  , трансцендентные
числа), их мощности. Теории действительных чисел Г.Кантора,
Р.Дедекинда, К.Вейерштрасса (исторический анализ, различие и
взаимосвязи).
, трансцендентные
числа), их мощности. Теории действительных чисел Г.Кантора,
Р.Дедекинда, К.Вейерштрасса (исторический анализ, различие и
взаимосвязи).
3. Принцип Архимеда. Позиционные системы счисления. Двоичная
система счисления и ЭВМ.
Формулировка и геометрическая трактовка принципа Архимеда.
Приложение принципа Архимеда. Плотность множества 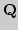 в
в 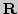 .
Рациональное приближение действительных чисел. Позиционная система
счисления, взаимный переход из одной системы счисления в другую.
Запись информации в память ЭВМ, понятие бита и байта информации.
.
Рациональное приближение действительных чисел. Позиционная система
счисления, взаимный переход из одной системы счисления в другую.
Запись информации в память ЭВМ, понятие бита и байта информации.
4. Отображения множеств, типы и классификация. Операции над
отображениями
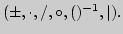
Отображение множеств (эволюция понятий, современная трактовка
понятия функции). Типы отображений: инъекция, сюръекция, биекция.
Классификация отображений:
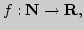
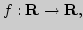
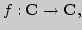
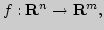
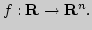 Операции над
отображениями: арифметические, композиции, обращение, сужение,
продолжение. Построить непрерывное продолжение показательной
функции
Операции над
отображениями: арифметические, композиции, обращение, сужение,
продолжение. Построить непрерывное продолжение показательной
функции 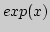 с
с 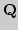 на
на 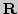 (провести доказательство
непрерывности и теоремы сложения).
(провести доказательство
непрерывности и теоремы сложения).
5. Основные элементарные функции, множество элементарных
функций. Классификация элементарных функций. Неэлементарные
функции.
Основные элементарные функции: постоянная, степенная,
показательная, логарифмическая, тригонометрические, обратные
тригонометрические; графики и основные свойства. Системы координат
на плоскости и в пространстве: декартова, полярная,
параметрическая, задание элементарных функций, взаимопереход
различных систем координат. Мера угла, построение
тригонометрических функций (вычисление площади сектора или длины
дуги). Многочлены, рациональные, иррациональные, алгебраические,
трансцендентные функции; примеры. Неэлементарные функции; примеры.
6. Элементарные функции в комплексной плоскости.
Основные элементарные функции в комплексной области:
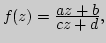
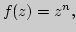
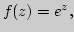
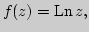
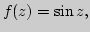 различные подходы к определению, идея
аналитического продолжения, свойства. Доказательство формулы
различные подходы к определению, идея
аналитического продолжения, свойства. Доказательство формулы
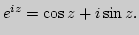
7. Аксиоматическое представление основных элементарных
функций. Формула и ряд Тейлора.
Линейное, квадратичное, полиномиальное приближение основных
элементарных функций. Формулы Лагранжа и Тейлора, ряд Тейлора.
Остаточные члены в форме Пеано и Лагранжа. Разложение основных
элементарных функций: 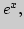
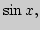

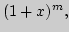
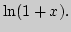 Единственность разложения в ряд Тейлора.
Единственность разложения в ряд Тейлора.
8. Предел функции в точке 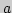 . Пространство
. Пространство 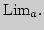 Односторонние и бесконечные пределы. Признаки существования
предела. Замечательные пределы.
Односторонние и бесконечные пределы. Признаки существования
предела. Замечательные пределы.
Предел функции в точке (окрестностное определение),
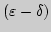 -язык, язык последовательностей (по Гейне).
Эквивалентность
-язык, язык последовательностей (по Гейне).
Эквивалентность
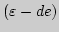 -языка и языка Гейне. Предел
последовательности. Алгебраическая структура
-языка и языка Гейне. Предел
последовательности. Алгебраическая структура 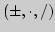 и
структура отношения порядка
и
структура отношения порядка 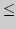 на множестве
на множестве 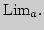 Замечательные пределы, число
Замечательные пределы, число 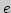 . Признаки существования предела.
. Признаки существования предела.
9. Топология числовой прямой. Окрестность точки в  Строение открытых и замкнутых множеств в
Строение открытых и замкнутых множеств в 
Окрестность точки в 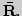 Отделимость окрестностей.
Классификация точек: предельная, внутренняя и граничные точки
множества. Строение открытых и замкнутых множеств в
Отделимость окрестностей.
Классификация точек: предельная, внутренняя и граничные точки
множества. Строение открытых и замкнутых множеств в  Методы
решения неравенств, содержащих модуль.
Методы
решения неравенств, содержащих модуль.
10. Метрические пространства 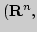
![$C_{[a;b]},$](img282.png)
![$C^1_{]a;b[},$](img283.png)
![$c^\infty_{]a;b[}$](img284.png) ). Сходимость в метрическом
пространстве. Полные метрические пространства. Метод
последовательных приближений.
). Сходимость в метрическом
пространстве. Полные метрические пространства. Метод
последовательных приближений.
Метрические пространства; примеры. Неравенство Коши-Буняковского.
Покоординатная сходимость, равномерная сходимость. интегральная
сходимость; примеры. Теорема Банаха. Сжимающие операторы в 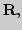 приложение к приближенному решению уравнения
приложение к приближенному решению уравнения 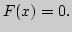 Вычисление
Вычисление
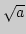 методом последовательных приближений.
методом последовательных приближений.
11. Непрерывность функции в точке метрического пространства.
Алгебраическая структура и полнота пространства ![$C_{[a;b]}.$](img287.png)
Непрерывность функции в метрическом пространстве
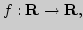
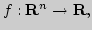
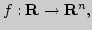
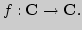 Непрерывность
основных элементарных функций. Алгебраическая структура
Непрерывность
основных элементарных функций. Алгебраическая структура
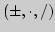 и полнота пространства
и полнота пространства ![$C+{[a;b]}$](img291.png) в равномерной
метрике. Использование непрерывности при нахождении предела
функции.
в равномерной
метрике. Использование непрерывности при нахождении предела
функции.
12. Свойства функций, непрерывных на отрезке. Метод
Больцано.
Теоремы Больцано-Коши и Вейерштрасса, непрерывность композиции и
обращение (доказательство теоремы Больцано-Коши методом
Больцано). Доказательство включения
![$C^1_{]a;b[}\subset
C_{]a;b[}.$](img292.png) Примеры непрерывных, но не дифференцируемых функций с
доказательством.
Примеры непрерывных, но не дифференцируемых функций с
доказательством.
Далее: Литература
Вверх: Дидактический модуль "Введение в
Назад: §3. Фрейм аннотированной учебной
ЯГПУ, Центр информационных технологий обучения
25.04.2008
![]() для числовой последовательности
для числовой последовательности
![]() (педагогический программный продукт) (2 часа)
(педагогический программный продукт) (2 часа)
![\fbox{\footnotesize
\unitlength=1.00mm
\special{em:linewidth 0.4pt}
\linethickne...
...0){\makebox(0,0)[cc]{*}}
\put(139.00,64.00){\makebox(0,0)[cc]{*}}
\end{picture}}](img1552.png)