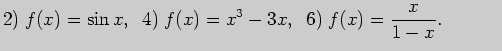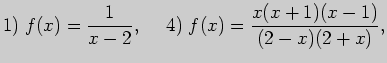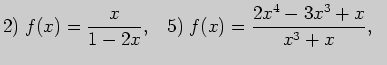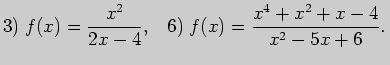Далее: 4. Интегрирование
Вверх: II. Элементы математического анализа
Назад: 2. Предел. Непрерывность
Вопросы теории. Задача о касательной к графику функции в
точке. Понятие производной функции в точке. Уравнения касательной
и нормали к графику функции в точке. Дифференцируемость функции и
ее связь с непрерывностью. Правила вычисления производных. Таблица
производных основных элементарных функций. Свойства функций,
непрерывных на отрезке и дифференцируемых внутри него. Правила
Лопиталя. Дифференциал и его геометрический смысл. Таблица
дифференциалов. Применение дифференциала к приближенным
вычислениям. Инвариантность формы первого дифференциала.
Производные и дифференциалы высших порядков. Экстремумы функции и
правила их вычисления. Наибольшее и наименьшее значения функции на
отрезке. Асимптоты графика функции и их вычисление.
Образцы решения задач
Задача 1. Вычислите уравнения касательной и нормали к графику функции
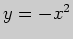 в точке
в точке 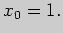
Решение. Угловой коэффициент касательной к графику функции в точке равен
значению производной в этой точке, поэтому
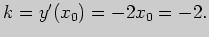 Обозначая
Обозначая
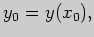 имеем
имеем
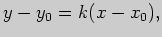 или, подставив числовые значения,
или, подставив числовые значения,
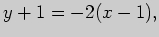
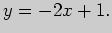 Для нахождения уравнения нормали воспользуемся
тем фактом, что ее угловой коэффициент
Для нахождения уравнения нормали воспользуемся
тем фактом, что ее угловой коэффициент 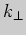 удовлетворяет соотношению
удовлетворяет соотношению
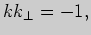 где
где 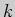 - угловой коэффициент касательной в той же точке.
Поэтому уравнение нормали имеет вид
- угловой коэффициент касательной в той же точке.
Поэтому уравнение нормали имеет вид
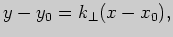
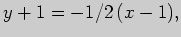
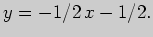
Задача 2. Вычислите производную функции
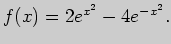
Решение. Пользуясь линейностью операции нахождения производной и правилом
дифференцирования сложной функции, получим
Задача 3. Пользуясь правилом Лопиталя, вычислите предел
Решение. Заменяя отношение бесконечно малых функций отношением их
производных, имеем
Задача 4. Пользуясь понятием дифференциала, вычислите приближенно
значение функции 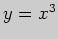 в точке
в точке
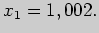
Решение. Найдем дифференциал данной функции:
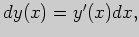
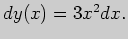 Тогда линейная часть приращения этой функции,
отвечающего конечному приращению независимой переменной
Тогда линейная часть приращения этой функции,
отвечающего конечному приращению независимой переменной 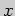 , имеет вид
, имеет вид
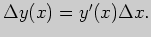 Значение функции в данной точке
Значение функции в данной точке
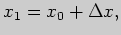
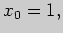
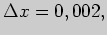 приближенно равно
приближенно равно
Задача 5. Исследуйте функцию
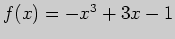 на монотонность и
экстремумы.
на монотонность и
экстремумы.
Решение. Функция задана многочленом, и поэтому она определена на всей
числовой прямой:
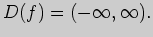 Вычислим производную:
Вычислим производную:
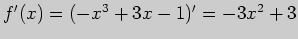 . Очевидно,
. Очевидно,
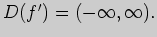 Найдем нули
производной:
Найдем нули
производной:
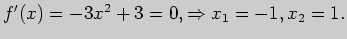 Эти точки разбивают
область определения функции
Эти точки разбивают
область определения функции 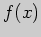 на интервалы, в которых производная сохраняет
знак. Определяя знаки производной и применяя достаточное условие экстремума,
получаем следующие результаты:
на интервалы, в которых производная сохраняет
знак. Определяя знаки производной и применяя достаточное условие экстремума,
получаем следующие результаты:
| |
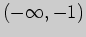 |
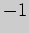 |
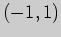 |
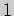 |
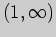 |
|
|
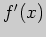 |
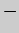 |
0 |
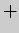 |
0 |
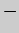 |
|
|
| |
|
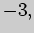 |
|
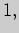 |
|
|
|
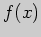 |
убывает |
локальный |
возрастает |
локальный |
убывает |
|
|
| |
|
минимум |
|
максимум |
|
|
|
Задача 6. Найдите наибольшее и наименьшее значения функции
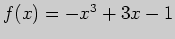 на отрезке
на отрезке ![$ [0,2]$](img399.png) .
.
Решение. В решении задачи 5 были найдены производная этой функции и
точки 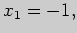
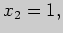 в которых производная обращается в нуль. Из этих
точек только
в которых производная обращается в нуль. Из этих
точек только 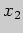 лежит в указанном интервале. Наибольшее и наименьшее
значения функции на данном отрезке равны
лежит в указанном интервале. Наибольшее и наименьшее
значения функции на данном отрезке равны
Задача 7. Исследуйте функцию
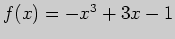 на выпуклость,
вогнутость и перегиб.
на выпуклость,
вогнутость и перегиб.
Решение. В решении задачи 5 указана область определения и найдена первая
производная этой функции. Вторая ее производная равна
и определена всюду на числовой прямой. Она обращается в нуль в точке 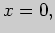 которая разбивает область определения на два интервала
которая разбивает область определения на два интервала
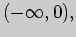
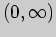 . В соответствии в достаточным
условием выпуклости, вогнутости и перегиба имеем
. В соответствии в достаточным
условием выпуклости, вогнутости и перегиба имеем
| |
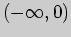 |
0 |
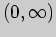 |
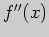 |
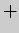 |
0 |
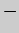 |
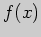 |
вогнута |
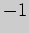 |
выпукла |
| |
|
перегиб |
|
Задача 8. Вычислите уравнения асимптот графика функции
Решение. Область определения данной функции 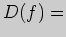
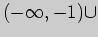
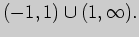 Вычислим односторонние пределы функции в точках
Вычислим односторонние пределы функции в точках
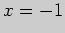 и
и 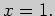
Таким образом, график функции 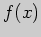 имеет две вертикальные асимптоты:
имеет две вертикальные асимптоты:
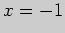 и
и 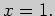 Уравнение наклонной (или горизонтальной) асимптоты
будем вычислять в виде
Уравнение наклонной (или горизонтальной) асимптоты
будем вычислять в виде 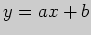 .
.
Итак, наклонная асимптота графика данной функции задана уравнением 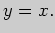
Задачи для самостоятельного решения
1. Напишите уравнения касательной и нормали к графику функции 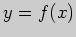 в точке
в точке 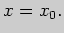
2. Вычислите производные функций:
3. Пользуясь правилами Лопиталя, вычислите пределы:
4. Пользуясь понятием дифференциала, вычислите приближенно значение
функции 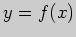 в точке
в точке 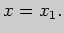 5. Исследуйте функции на монотонность и экстремумы:
5. Исследуйте функции на монотонность и экстремумы:
6. Укажите наибольшее и наименьшее значения функции на отрезке:
7. Вычислите вторую производную функции. Исследуйте функцию на выпуклость,
вогнутость и перегиб:
8. Вычислите уравнения асимптот графика функции:
Далее: 4. Интегрирование
Вверх: II. Элементы математического анализа
Назад: 2. Предел. Непрерывность
ЯГПУ, Центр информационных технологий обучения
27.03.2007
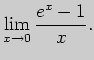
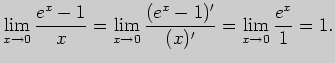
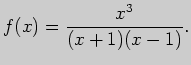
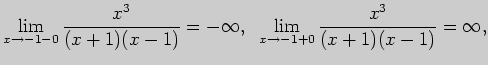
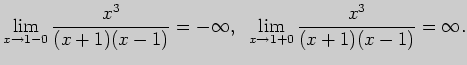
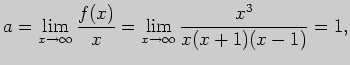
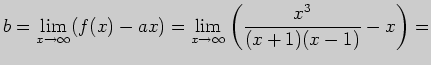
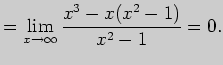
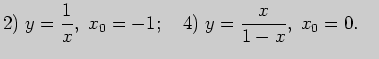
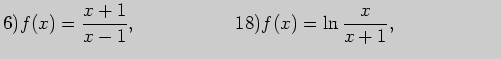
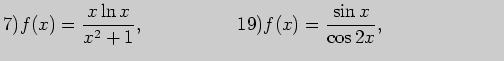
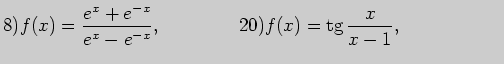
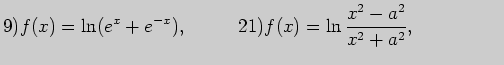
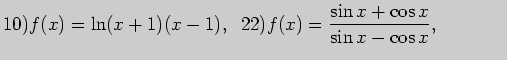
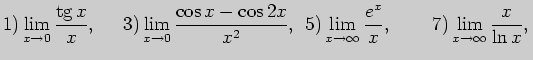
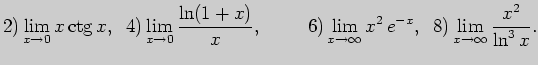
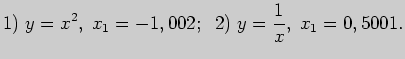
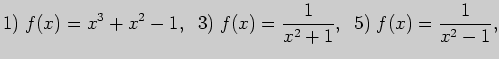
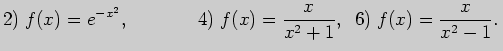
![$\displaystyle 1)\; y=-x^2,\;[-1,2];\;\;
2)\; y=\cos x,\;\left[ \frac{3\pi}{4}, \frac{3\pi}{2}\right]; \;\;
3)\; y=x \sin x,\;[0,\pi].
$](img445.png)