Далее: 3. Производная и ее
Вверх: II. Элементы математического анализа
Назад: 1. Элементарные функции и
Вопросы теории. Понятия предела числовой последовательности
и предела функции в точке. Предел функции на бесконечности. Понятие бесконечно
малой и бесконечно большой (в точке) функции. Правила вычисления пределов
суммы, разности, произведения и частного двух функций. Понятие функции,
непрерывной в точке области определения. Функция, непрерывная на промежутке.
Свойства функций, непрерывных на отрезке. Связь непрерывности с операциями
над функциями. Непрерывность элементарных функций в их областях определения.
Непосредственное вычисление предела непрерывной функции в точке ее области
определения. Простейшие виды неопределенностей и методы их раскрытия. Первый
и второй замечательные пределы. Разрывы функции и их классификация.
Образцы решения задач
Задача 1. Вычислите, пользуясь непрерывностью элементарных функций
в их областях определения:
Решение. Знаменатель выражения под знаком предела не обращается в нуль
при  ; числитель тоже определен в этой точке. Все элементарные функции
непрерывны в областях определения. Согласно определению функции, непрерывной
в точке, ее предел в точке равен значению в этой точке. Поэтому
; числитель тоже определен в этой точке. Все элементарные функции
непрерывны в областях определения. Согласно определению функции, непрерывной
в точке, ее предел в точке равен значению в этой точке. Поэтому
Задача 2. Вычислите пределы
Решение. 1) Выражение под знаком предела представляет собой
отношение бесконечно больших функций.
2) Введем новую переменную  замечая, что
замечая, что
 :
3) Введем новую переменную
:
3) Введем новую переменную 
 и воспользуемся вторым
замечательным пределом:
и воспользуемся вторым
замечательным пределом:
Задача 3. Найдите точки разрыва функции
и укажите их тип.
Решение. Найдем область определения данной функции:
 Элементарные функции, которыми
задается данная функция на разных подмножествах области определения, не
имеют точек разрыва в соответствующих им интервалах. Поэтому достаточно
исследовать данную функцию на непрерывность в точках
Элементарные функции, которыми
задается данная функция на разных подмножествах области определения, не
имеют точек разрыва в соответствующих им интервалах. Поэтому достаточно
исследовать данную функцию на непрерывность в точках  и
и  . Для этого
вычислим односторонние пределы функции
. Для этого
вычислим односторонние пределы функции 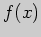 в этих точках.
Односторонние пределы в точке
в этих точках.
Односторонние пределы в точке  конечны, в то время как в этой точке
функция не определена, поэтому
конечны, в то время как в этой точке
функция не определена, поэтому  - точка разрыва первого рода. Они равны,
поэтому это - точка устранимого разрыва, и, доопределив данную функцию в нуле
выражением
- точка разрыва первого рода. Они равны,
поэтому это - точка устранимого разрыва, и, доопределив данную функцию в нуле
выражением  получим функцию, непрерывную в точке
получим функцию, непрерывную в точке  Один из односторонних пределов в точке
Один из односторонних пределов в точке  бесконечен, поэтому это - точка
разрыва второго рода.
бесконечен, поэтому это - точка
разрыва второго рода.
Задачи для самостоятельного решения
1. Вычислите пределы, пользуясь непрерывностью входящих в них функций.
2. Укажите промежутки непрерывности функций
3. Вычислите, используя, где это необходимо, первый и второй
замечательные пределы:
4. Определите тип точек разрыва функций, данных в задаче 2. В точках
устранимого разрыва доопределите функции так, чтобы они стали непрерывными.
Далее: 3. Производная и ее
Вверх: II. Элементы математического анализа
Назад: 1. Элементарные функции и
ЯГПУ, Центр информационных технологий обучения
27.03.2007



















