Далее: Лекция 4. Симплексы и Вверх: Дифференциальная геометрия и элементы Назад: Лекция 2. Непрерывные отображения

Лекция 3. Топологические и дифференцируемые многообразия

План. Понятие топологического многообразия. Топологические многообразия с краем. Размерность топологического многообразия. Топологические подмногообразия размерностей 1 и 2 в вещественном евклидовом пространстве. Связная сумма топологических многообразий. Понятие дифференцируемого многообразия. Координатные функции и функции перехода. Примеры дифференцируемых многообразий.

Цель лекции - аксиоматизировать привычные черты кривых и поверхностей и ввести топологический объект, локально устроенный как евклидово пространство, а также подготовить методологическую базу для применения аппарата математического анализа в геометрии.

(Вещественным) топологическим многообразием (без края) называется хаусдорфово топологическое пространство $(X, \tau)$ со счетной базой, каждая точка которого обладает окрестностью, гомеоморфной евклидову пространству ${\mathbb{R}}^n$. Число $n$ называется размерностью топологического многообразия $X$.

Иногда удобнее использовать равносильную форму определения многообразия.

(Вещественным) топологическим многообразием (без края) называется хаусдорфово топологическое пространство $(X, \tau)$ со счетной базой, локально гомеоморфное евклидову пространству ${\mathbb{R}}^n$.

Важно, что топологические многообразия локально устроены как евклидовы пространства подходящей размерности. Однако можно построить топологические пространства, удовлетворяющие требованиям хаусдорфовости, локально гомеоморфные евклидову пространству, но не являющиеся многообразиями.

Простейший пример такого топологического пространства поставляет объединение всех параллельных прямых на евклидовой плоскости, заданных уравнениями $y=\alpha,$ где $\alpha$ - иррациональное число. Каждая из этих прямых удовлетворяет всем требованиям для топологического многообразия. Объединение всех прямых с иррациональными ординатами является хаусдорфовым пространством, локально гомеоморфным числовой прямой ${{\mathbb{R}}}={{\mathbb{R}}}^1$. Однако на таком объединении невозможно ввести счетную базу топологии. Чтобы убедиться в этом, зафиксируем на каждой из прямых какую-нибудь счетную бесконечную базу. Очевидно, объединение баз по всем прямым рассматриваемого набора несчетно, так как его мощность не меньше мощности множества иррациональных чисел.

Простейшими примерами топологических многообразий являются числовая прямая с классической топологией, окружность и евклидова плоскость. Более содержательный пример - двумерный тор $T^{ 2}=S^1\times S^1$. В лекции 2 рассмотрен пример локального гомеоморфизма тора и евклидовой плоскости. Тор - хаусдорфово пространство (рис. 7).

Тор как хаусдорфово пространство

Для поверки этого факта рассмотрим две различные точки $p$ и $q$ тора, вложенного в трехмерное евклидово пространство ${{\mathbb{R}}}^3$ способом, описанным в лекции 2. Пространство ${{\mathbb{R}}}^3$, как известно читателю, является метрическим. Поэтому в качестве непересекающихся окрестностей точек $p$ и $q$ в пространстве ${{\mathbb{R}}}^3$ можно выбрать открытые шары достаточно малого радиуса $r$. Тогда искомые непересекающиеся окрестности точек $p$ и $q$ на торе представлены его пересечениями с открытыми шарами.

Тор - топологическое пространство, допускающее счетную базу. Для ее построения зафиксируем счетную базу классической топологии в трехмерном евклидовом пространстве. Затем в качестве множеств, образующих базу на торе, возьмем пересечения тора и множеств базы топологии трехмерного пространства.

Упражнение. Пользуясь определением, убедитесь в том, что такие пересечения действительно образуют базу топологии тора.

Понятно, что построенная таким способом база топологии тора имеет мощность, не превосходящую мощность базы топологии трехмерного евклидова пространства, то есть является счетной. Таким образом, двумерный тор - хаусдорфово пространство со счетной базой, локально гомеоморфное евклидовой плоскости, то есть он является топологическим многообразием размерности два.

Примеры многообразий с краем: а) полупрямая, б) тор с удаленным диском, в) лента Мебиуса

(Вещественным) топологическим многообразием c краем называется хаусдорфово топологическое пространство $(X, \tau)$ со счетной базой, каждая точка которого принадлежит одному из двух следующих классов:
1) класс точек, каждая из которых обладает окрестностью, гомеоморфной евклидову пространству ${\mathbb{R}}^n$;
2) класс точек, каждая из которых обладает окрестностью, гомеоморфной полупространству ${\mathbb{R}}^n_+=\{(x_1,x_2, \dots x_n)\in {\mathbb{R}}^n\vert x_1\ge 0\}$ евклидова пространства ${\mathbb{R}}^n$.

Точки первого класса называются внутренними точками многообразия $X$, точки второго класса - точками границы или точками края. Число $n$ называется размерностью топологического многообразия $X$.

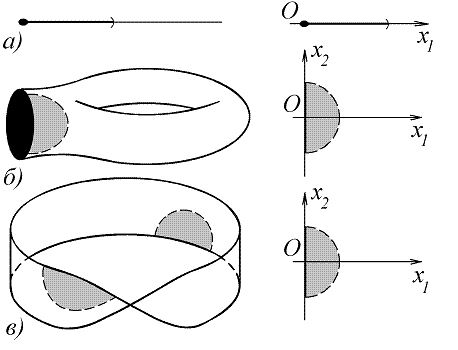
Примерами одномерных многообразий с краем служат отрезок и полупрямая, примерами двумерных - круг, тор с удаленным диском и лента Мебиуса (рис. 8). Границы трех последних многообразий гомеоморфны окружности, в то время как сами многообразия негомеоморфны.

Для конструирования топологических многообразий часто используется операция приклеивания, заключающаяся в следующем. Пусть $X$ и $Y$ - топологические многообразия, $Z_X\subset X$, $Z_Y \subset Y$ - подмножества, причем $Z_X$ гомеоморфно $Z_Y$. Пусть $f: Z_X\to Z_Y$ - гомеоморфизм. Отождествляя каждую точку $x\in Z_X$ с ее образом $f(x)\in Z_Y$, получим новое многообразие $X\coprod _f Y$, называемое склейкой многообразий $X$ и $Y$ вдоль гомеоморфизма $f$.

Построим с помощью этой операции двумерное многообразие, играющее важную роль в различных областях математики - вещественную проективную плоскость ${{\mathbb{R}}}\!P^2$.

Вещественная проективная плоскость

Построение начинается с полусферы, например, заданной условиями $x^2+y^2+z^2=1,\;\; z\le 0.$ Ее границей является окружность $x^2+y^2=1,\;\; z=0,$ получаемая в пересечении сферы плоскостью $xOy$ (экватор). Рассмотрим гомеоморфизм границы полусферы на себя, задаваемый центральной симметрией относительно начала координат $f: (x,y,0)\mapsto (-x,-y,0).$ Вещественная проективная плоскость получается склеиванием экватора полусферы вдоль гомеоморфизма $f$ (рис. 9). Для получения другой интерпретации вещественной проективной плоскости рассмотрим трехмерное аффинное пространство. На множестве всех прямых этого пространства определено отношение параллельности, которое, как хорошо известно читателю, является отношением эквивалентности. Тогда имеется разбиение множества всех прямых трехмерного пространства на классы параллельности. Каждый такой класс состоит из (бесконечного!) набора всех прямых пространства, имеющих данное направление. Класс параллельных прямых может быть задан направляющим вектором прямой этого класса. Выбор направляющего вектора не однозначен; все направляющие векторы данной прямой (и данного класса параллельных прямых) коллинеарны и имеют ненулевую длину. Тогда каждый класс параллельных прямых задается направлением, то есть классом ненулевых коллинеарных векторов.

Проективная плоскость - это многообразие, точки которого соответствуют классам параллельных прямых трехмерного аффинного пространства или, равносильно, классам коллинеарности ненулевых векторов трехмерного векторного пространства. Зафиксируем в нем базис; тогда каждый вектор $\vec a\ne \vec 0$ задается координатами $\vec a=(a_0,a_1,a_2)$, причем хотя бы одна из координат отлична от нуля.

Соответствие между направлениями и точками проективной плоскости

Векторы, принадлежащие одному направлению, имеют пропорциональные координаты, поэтому направление может быть задано способом, известным из курса проективной геометрии как однородные координаты. Однородные координаты $(a_0:a_1:a_2)$ - это класс пропорциональных упорядоченных троек чисел, хотя бы одно из которых отлично от нуля. Каждый из таких классов определяет направление и, следовательно, точку проективной плоскости. Это соответствие представлено на рис. 10. Направления изображены в виде прямых, проходящих через начало координат и пересекающих полусферу, из которой проективная плоскость получалась путем склейки границы. Каждая из прямых, не принадлежащих плоскости экваториального сечения (плоскости $xOy$), пересекает полусферу в единственной точке и таким образом выделяет точку проективной плоскости, отвечающую данному направлению. Каждая прямая, принадлежащая плоскости экваториального сечения, пересекает полусферу в двух точках границы, отождествляемых склейкой, и, тем самым, также выделяет единственную точку проективной плоскости.

Связная сумма топологических многообразий

Для построения связной суммы многообразий $X$ и $Y$ одинаковой размерности $n$ выберем окрестности $B_x$ и $B_y$ точек $x\in X$ и $y\in Y$ соответственно, гомеоморфные открытому $n$-мерному шару. Очевидно, границы многообразий $X\backslash B_x$ и $Y\backslash B_y$ гомеоморфны ($n-1$-мерной сфере). Пусть $f$ - какой-нибудь гомеоморфизм границ. Тогда связная сумма $X\sharp Y$ многообразий $X$ и $Y$ определяется как их склейка вдоль гомеоморфизма $f$ (рис. 11).

Координатные отображения и отображения склейки

Топологическое многообразие $X$ называется дифференцируемым класса $C^k$ (или $C^{\infty}$), если гомеоморфные отображения $f_i: U_i \to {\mathbb{R}}^n$ подчинены следующему условию: для любых $i,j$ ограничения отображений $f_i$ и $f_j$ согласованы в следующем смысле: определено отображение $\varphi_{ij}:= f_j{{\mbox{\scriptsize $\circ $}}}(f_i\vert _{U_i \cap U_j})^{-1}: f_i(U_i \cap U_j) \to f_j(U_i \cap U_j)$, задаваемое функциями, имеющими непрерывные частные производные порядка $k$ (соответственно, имеющими непрерывные частные производные любого порядка), такое, что $f_j\vert(U_i \cap U_j)=\varphi_{ij} {{\mbox{\scriptsize $\circ $}}} (f_i\vert(U_i \cap U_j))$ (рис. 12). Отображения $f_i$ называются координатными отображениями, пара $(U_i, f_i)$ - картой, а соответствующий покрытию $\{U_i\}_{i\in I}$ набор $\{(U_i, f_i)\}$ - атласом дифференцируемого многообразия $X$. Отображения $\varphi_{ij}$ иногда называют отображениями склейки.

Многообразия класса $C^{\infty}$ называют также аналитическими.

В качестве примера снабдим двумерный тор структурой дифференцируемого многообразия. В лекции 3 доказан локальный гомеоморфизм тора и евклидовой плоскости. Атлас на торе может быть построен выбором различных начал отсчета угловых координат $\varphi$ и $\psi$. Рассмотрим построение атласа на торе подробнее. Назовем параллелью геометрическое место точек тора, имеющих одно и то же значение угловой координаты $\psi$; меридианом - геометрическое место точек тора, имеющих одно и то же значение угловой координаты $\varphi$, то есть любую его образующую.

Выбор координатной карты на торе

Разрезав тор вдоль выбранных параллели и меридиана (рис. 13), получим множество точек, гомеоморфное прямоугольнику, называемому разверткой тора. Введем (новые) координаты на развертке так, что $\psi=\pm \pi$ соответствует параллели разреза, $\varphi=0$ и $\varphi=2\pi$ - меридиану разреза. Прямоугольник $0<\varphi<2\pi,$ $-\pi<\psi< \pi$ c гомеоморфизмом в тор образует координатную карту.

Атлас на торе

Выберем три пары параллель-меридиан, причем так, что все три параллели и все три меридиана различны (рис. 14). Каждая такая пара задает способ отсчета угловых координат на торе только что описанным образом, причем каждая точка тора покрыта хотя бы одной из трех карт. Пусть $U_1$ и $U_2$ - две построенные таким способом координатные карты, и точка с координатами $_1\varphi=0, \;_1\psi=0$ в карте $U_1$ имеет в карте $U_2$ координаты $_2\varphi=\varphi_0, \;_2\psi=\psi_0$. Тогда имеют место уравнения перехода от координат $(_1\varphi, \;_1\psi)$ в карте $U_1$ к координатам $(_2\varphi, \;_2\psi)$ в карте $U_2$:

$$_2\varphi=_{1\!}\varphi+\varphi_0, \;_2\psi=_{1\!}\psi+\psi_0.$$

Очевидно, что отображение склейки, заданное этими уравнениями, имеет производные любого порядка, и построенная нами структура вещественного многообразия на двумерном торе является, согласно определению, структурой аналитического многообразия.

Структуры дифференцируемых многообразий нетрудно ввести, например, на сфере, параболоиде вращения и других известных читателю поверхностях второго порядка.

Упражнение. С помощью однородных координат построим локальные карты на проективной плоскости. Карта $^0U$ соответствует множеству точек с ненулевой координатой $a_0$; координаты в этой карте имеют вид $^0x=a_1/a_0,\; ^0y=a_2/a_0$. Аналогично, $^1U: a_1\ne 0, ^1x=a_0/a_1,\; ^1y=a_2/a_1.$ Также, $^2U: a_2\ne 0, ^1x=a_0/a_2,\; ^1y=a_1/a_2.$ Выпишите функции перехода и убедитесь в том, что вещественная проективная плоскость ${{\mathbb{R}}}P^2$ - аналитическое многообразие.

Далее: Лекция 4. Симплексы и Вверх: Дифференциальная геометрия и элементы Назад: Лекция 2. Непрерывные отображения