Пусть {![]() ,
, ![]() , ...,
, ...,![]() } - множество состояний
некоторой физической системы. В любой момент времени система может
находиться в одном состоянии и меняет свое состояние только в моменты
} - множество состояний
некоторой физической системы. В любой момент времени система может
находиться в одном состоянии и меняет свое состояние только в моменты
![]() ,
, ![]() , ...,
, ..., ![]() , .... Для
однородных цепей Маркова
вероятность
, .... Для
однородных цепей Маркова
вероятность ![]() перехода системы из состояния
перехода системы из состояния ![]() в состояние
в состояние
![]() за один шаг зависит только от того, из какого
состояния в какое
осуществлялся переход.
за один шаг зависит только от того, из какого
состояния в какое
осуществлялся переход.
Вероятности перехода ![]() удобно располагать в виде
матрицы. Обозначим ее
удобно располагать в виде
матрицы. Обозначим ее
![\begin{displaymath}
{\bf P}=\left[\matrix{p_{11}&p_{12}&...&p_{1k}\cr
p_{21}&p_{...
...p_{2k}\cr
...&...&&...\cr
p_{k1}&p_{k2}&...&p_{kk}\cr
}\right]
\end{displaymath}](img467.png)
а) ![]() б)
б) 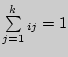 (
(![]() =
1, 2, ...,
=
1, 2, ..., ![]() ;
;
т.е. сумма элементов каждой строки матрицы перехода равна единице. Квадратные матрицы, для которых выполняются условия а) и б), называются стохастическими.
Вектор ![]() , где
, где
![]() -
вероятность появления состояния
-
вероятность появления состояния ![]() (
(![]() = 1,
2, ...,
= 1,
2, ..., ![]() в начальном
испытании, называется вектором начальных вероятностей.
в начальном
испытании, называется вектором начальных вероятностей.
Свойства однородных марковских цепей полностью определяются
вектором начальных вероятностей и матрицей вероятностей перехода.
В некоторых случаях вместо матрицы P используют
ориентированный граф, вершинами которого являются состояния цепи,
а стрелка, идущая от состояния ![]() в состояние
в состояние ![]() с
числом
с
числом ![]() рядом с ней, показывает, что из
состояния
рядом с ней, показывает, что из
состояния ![]() возможен переход в состояние
возможен переход в состояние ![]() с
вероятностью
с
вероятностью ![]() . В
том случае, когда
. В
том случае, когда ![]() 0, соответствующее ребро не
проводится.
В случае однородных цепей Маркова с вектором начальных
вероятностей появляется еще начальная вершина графа, которая
соединяется с состоянием
0, соответствующее ребро не
проводится.
В случае однородных цепей Маркова с вектором начальных
вероятностей появляется еще начальная вершина графа, которая
соединяется с состоянием ![]() ребром с числом
ребром с числом ![]() рядом с
ним.
рядом с
ним.
Можно показать, что матрица перехода P![]() за
за ![]() шагов находится как
шагов находится как ![]() .
.
Если из состояния ![]() система может перейти в
состояние
система может перейти в
состояние ![]() с
положительной вероятностью за конечное число шагов, то говорят, что
с
положительной вероятностью за конечное число шагов, то говорят, что
![]() достижимо из
достижимо из ![]() .
Состояние
.
Состояние ![]() называется существенным, если
для
каждого
состояния
называется существенным, если
для
каждого
состояния ![]() , достижимого из
, достижимого из![]() достижимо из
достижимо из ![]() . В противном
случае
. В противном
случае ![]() называется несущественным
состоянием.
называется несущественным
состоянием.
Понятие марковской цепи принадлежит русскому математику А.А. Маркову, чьи первые статьи по этому вопросу при решении лингвистических проблем были опубликованы в 1906-1908 гг.
Пример 51. Частица, находящаяся на прямой, движется по
этой прямой под влиянием случайных толчков, происходящих в моменты
![]() ,
, ![]() ,
, ![]() ,
...Частица может находиться в
точках с целочисленными координатами 1, 2, 3, 4, 5; в точках 1 и 5
находятся отражающие стенки. Каждый толчок перемещает частицу
вправо с вероятностью
,
...Частица может находиться в
точках с целочисленными координатами 1, 2, 3, 4, 5; в точках 1 и 5
находятся отражающие стенки. Каждый толчок перемещает частицу
вправо с вероятностью ![]() и влево с вероятностью
и влево с вероятностью ![]() , если частицы
не находятся у стенки. Если же частица находится у стенки, то
любой толчок переводит ее на единицу внутрь промежутка [1,5].
Найти матрицу перехода P и ей соответствующий граф.
, если частицы
не находятся у стенки. Если же частица находится у стенки, то
любой толчок переводит ее на единицу внутрь промежутка [1,5].
Найти матрицу перехода P и ей соответствующий граф.
Решение. Пусть ![]() ,
, ![]() = 1,
2, 3, 4, 5. Тогда граф перехода выглядит
следующим образом:
= 1,
2, 3, 4, 5. Тогда граф перехода выглядит
следующим образом:
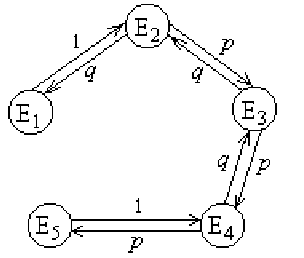
а матрица перехода -
![\begin{displaymath}
\begin{array}{@{\extracolsep{-5pt}}cccl}
&&& E_{1} E_{2} E...
... \\
0&0&q&0&p \\
0&0&0&1&0 \\
\end{array}\right]
\end{array}\end{displaymath}](img481.png)
Пример 52. Вероятности перехода за один шаг в цепях Маркова задаются матрицей:
![\begin{displaymath}
\begin{array}{@{\extracolsep{-5pt}}cccl}
&&& E_{1} ...
...
0&0&2/3&1/3 \\
0&0&1/2&1/2 \\
\end{array}\right]
\end{array}\end{displaymath}](img482.png)
Требуется:
а) найти число состояний;
б) установить, сколько среди них существенных и несущественных;
в) построить граф, соответствующий матрице P.
Решение.
а) 4 состояния.
б) состояния ![]() ,
, ![]() несущественны, поскольку остальные состояния
достижимы из них, но
несущественны, поскольку остальные состояния
достижимы из них, но ![]() недостижимо из
недостижимо из ![]() , а
, а ![]() недостижимо из
недостижимо из
![]() ; состояния
; состояния ![]() и
и ![]() являются существенными.
являются существенными.
в)
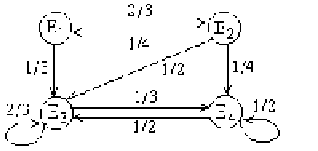
Пример 53 (задача о скрещивании). В близко родственном
скрещивании две особи, и среди их прямых потомков случайным
образом выбираются две особи разного пола. Они вновь скрещиваются,
и процесс этот продолжается бесконечно. Каждый родительский ген
может передаваться с вероятностью ![]() , и
последовательные испытания независимые. Имея три генотипа AA, Aа,
аа для каждого родителя, мы можем различать шесть комбинаций
родителей, которые пометим следующим образом:
, и
последовательные испытания независимые. Имея три генотипа AA, Aа,
аа для каждого родителя, мы можем различать шесть комбинаций
родителей, которые пометим следующим образом:
![]() =AA
=AA ![]() AA,
AA, ![]() = AA
= AA ![]() Aа,
Aа, ![]() =
AA
=
AA
![]() аа,
аа, ![]() = Aа
= Aа ![]() Aа,
Aа, ![]() = Aа
= Aа ![]() аа,
аа,
![]() = аа
= аа ![]() аа. Найдите граф и
матрицу перехода.
аа. Найдите граф и
матрицу перехода.
Решение.
![]() Рассмотрим, какое
потомство и с какой вероятностью может быть у особей разного пола, если
они
выбираются из
Рассмотрим, какое
потомство и с какой вероятностью может быть у особей разного пола, если
они
выбираются из ![]() .
.
Пусть ![]() = {
= {![]() -й потомок},
-й потомок}, ![]() = 1,
2 и
= 1,
2 и ![]() ,
,
![]() - разного пола, тогда варианты потомков и их
вероятности
можно найти по следующему графу:
- разного пола, тогда варианты потомков и их
вероятности
можно найти по следующему графу:
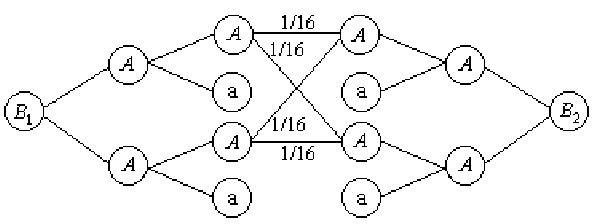
Получаем, что
![]()
![]()
![]()
Аналогично, находим и вероятности других переходов:
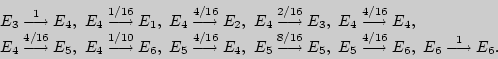
Тогда искомый граф перехода выглядит следующим образом:
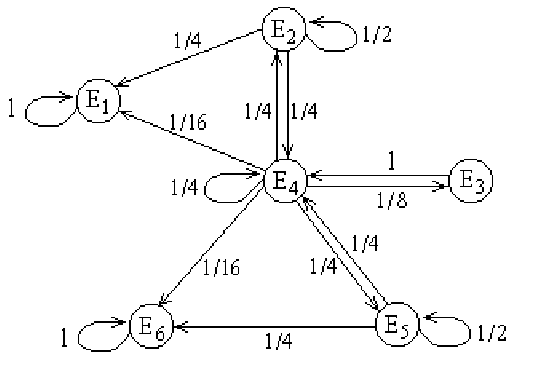
а матрица перехода -
![\begin{displaymath}
{\bf P}=\left[\matrix{1& 0& 0& 0& 0&
0 \cr
1/4&1/2&0&1/4&0&0...
.../4&1/4&1/16\cr
0&0&0&1/4&1/2&1/4\cr
0&0&0&0&0&1 \cr
}
\right].
\end{displaymath}](img500.png)
Пример 54. Матрица вероятностей перехода цепи Маркова имеет вид:
![\begin{displaymath}
{\bf P}=\left[\matrix{
0,2&0,3&0,5 \cr
0,5& 0,2&0,3 \cr
0,6&0,1&0,3 \cr
}
\right].
\end{displaymath}](img501.png)
Распределение по состояниям в момент времени ![]() = 0
определяется вектором
= 0
определяется вектором
![]() .
Найти распределения по состояниям в момент
.
Найти распределения по состояниям в момент ![]() = 2.
= 2.
Решение. Построим граф, соответствующий вектору начальных вероятностей и матрице перехода:
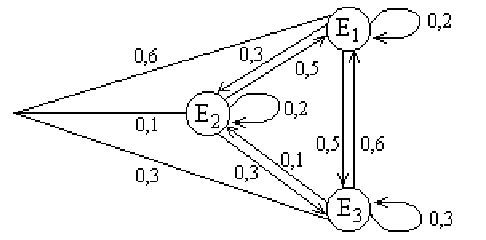
По этому графу находим распределение по состояниям в момент ![]() = 2:
= 2:
![]() = (0,6
= (0,6![]() (0,2)
(0,2)![]() +
0,6
+
0,6![]() 0,3
0,3![]() 0,5+0,6
0,5+0,6![]() 0,5
0,5![]() 0,6)+(0,1
0,6)+(0,1![]() 0,5
0,5![]() 0,2+0,1
0,2+0,1![]() 0,2
0,2![]() 0,5
+0,1
0,5
+0,1![]() 0,3
0,3![]() 0,6)+(0,3
0,6)+(0,3![]() 0,6
0,6![]() 0,2+(0,3)
0,2+(0,3)![]() 0,6)+(0,3
0,6)+(0,3![]() 0,1
0,1![]() 0,5)=0,437;
0,5)=0,437;
![]() = (0,1
= (0,1![]() (0,2)
(0,2)![]() +0,1
+0,1![]() 0,5
0,5![]() 0,3+0,1
0,3+0,1![]() 0,3
0,3![]() 0,1)+0,6
0,1)+0,6![]() 0,3
0,3![]() 0,2+0,6
0,2+0,6![]() 0,2
0,2![]() 0,3
+0,6
0,3
+0,6![]() 0,5
0,5![]() 0,1)+(0,3
0,1)+(0,3![]() 0,1
0,1![]() 0,2+(0,3)
0,2+(0,3)![]() 0,1+0,3
0,1+0,3![]() 0,6
0,6![]() 0,3)=0,193;
0,3)=0,193;
![]() = 0,37.
= 0,37.
Пример 55. Доказать, что P![]() =
P
=
P![]() для двух состояний цепи Маркова.
для двух состояний цепи Маркова.
Решение. Пусть цепь Маркова с двумя состояниями ![]() и
и ![]() задана своей матрицей перехода P:
задана своей матрицей перехода P:
Докажем утверждение методом математической индукции.
Пусть ![]() = 2. Тогда
= 2. Тогда
Вероятности перехода за два шага удобно находить по графу перехода:
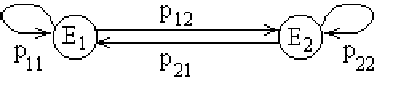
![\begin{displaymath}
{\bf P}^2=
\begin{array}{@{\extracolsep{-5pt}}cccl}
&&&\qqua...
..._{21}\cdot p_{12}+p_{22}^{2}\\
\end{array}\right].
\end{array}\end{displaymath}](img514.png)
Следовательно, P![]() = P
= P![]() ,
и
первый шаг метода
математической индукции выполняется. Предположим далее, что при
,
и
первый шаг метода
математической индукции выполняется. Предположим далее, что при ![]() проверяемое утверждение истинно, т.е. P
проверяемое утверждение истинно, т.е. P![]() =
P
=
P![]() , тогда матрица перехода за
, тогда матрица перехода за ![]() +1
шаг
P
+1
шаг
P![]() = P
= P![]() P =
P
P =
P![]() P = P
P = P![]() , что и
требовалось доказать.
, что и
требовалось доказать.
Вопросы для самоконтроля
Задачи
![\begin{displaymath}
{{\bf P}} = \left[ {\begin{array}{ccc}
1 / 2&1 / 3&1/6 \\
1 / 2&1 / 3&1/6 \\
1 / 2&1 / 3&1/6 \\
\end{array}} \right].
\end{displaymath}](img523.png)
Чему равно число состояний? Найти вероятности перехода из одного состояния в другое за два шага.
![\begin{displaymath}
{{\bf P}} = \left[ {\begin{array}{ccc}
0,4&0,5&0,1 \\
0,2&0,3&0,5\\
0,3&0,4&0,3 \\
\end{array}}\right].
\end{displaymath}](img526.png)
Вектор начальных вероятностей
![]() Найти вероятность
того, что через два шага система будет находиться в состоянии
Найти вероятность
того, что через два шага система будет находиться в состоянии ![]() .
.
![\begin{displaymath}
\left[\matrix{
0&2/5&3/5&0\cr
1/4&3/4&0&0\cr
0&2/3&0&1/3\cr
0&1/2&0&1/2\cr}
\right].
\end{displaymath}](img528.png)
Найти число состояний и определить среди них существенные и несущественные. Построить граф, соответствующий матрице P.
а)
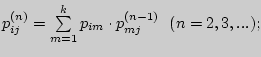
б) P![]() = P
= P![]() .
.