Далее: §35. Выборочный коэффициент корреляции Вверх: Глава V. Математическая статистика Назад: §33. Выборочные характеристики вариационного

§34. Доверительный интервал

Доверительным называется интервал, который с заданной надежностью $\alpha$ покрывает оцениваемый параметр.

Для оценки математического ожидания $a$ случайной величины $Х$, распределенной по нормальному закону, при известном среднем квадратическом отклонении $\sigma$ служит доверительный интервал

$$x^\ast - t{\displaystyle \sigma \over\displaystyle \sqrt n }... ... x^\ast + t{\displaystyle \sigma \over\displaystyle \sqrt n },$$

где $t{\displaystyle \sigma \over\displaystyle \sqrt n } = \delta$ - точность оценки, $n$ - объем выборки, $х^{\ast }$ - выборочное среднее, $t$ - аргумент функции Лапласа, при котором $\Phi (t) = {\displaystyle \alpha \over\displaystyle 2}.$

Пример 166. Найти доверительный интервал для оценки с надежностью 0,9 неизвестного математического ожидания $a$ нормально распределенного признака $Х$ генеральной совокупности, если среднее квадратическое отклонение $\sigma = 5$, выборочная средняя $х^{\ast } = 20$ и объем выборки $n = 100$.

Решение. Требуется найти доверительный интервал

$$x^\ast - t{\displaystyle \sigma \over\displaystyle \sqrt n }... ... x^\ast + t{\displaystyle \sigma \over\displaystyle \sqrt n }.$$

Все величины, кроме $t$, известны. Найдем $t$ из соотношения $\Phi(t) = 0,9/2= 0,45$.

По таблице приложения $2$ находим $t = 1,65$ и получаем доверительный интервал $19,175 < a < 20,825$.

Если среднее квадратическое отклонение $\sigma$ неизвестно, то для оценки $M[X] = a$ служит доверительный интервал

$$x^\ast - t_\alpha {\displaystyle \bar {s}\over\displaystyle ... ... t_\alpha {\displaystyle \bar {s}\over\displaystyle \sqrt n },$$

где $t_{\alpha }$ находится в приложении 4 по заданным $n$ и $\alpha$, а вместо $\bar {s}$ часто бывает возможно подставить любую из оценок

$$s = \sqrt {{\displaystyle 1\over\displaystyle n - 1}\sum\lim... ...style n}\sum\limits_{i = 1}^n {(x_i - x^\ast )^2 \cdot m_i } }$$

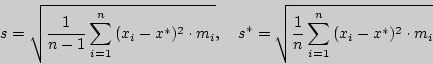
- исправленное среднеквадратическое, статистическое среднеквадратическое отклонения соответственно. При увеличении $n$ обе оценки $s$ и $s^{\ast }$ будут различаться сколь угодно мало и будут сходиться по вероятностям к одной и той же величине $\sigma$.

Пример 167. Из генеральной совокупности извлечена выборка объема

$n$ = 50:

$x_{i}$	-1	0	1	2	3
$m_{i}$	10	5	15	15	5

Оценить с надежностью $0,95$ математическое ожидание $a$ нормально распределенного признака генеральной совокупности по выборочной средней.

Решение. Выборочную среднюю и исправленное среднее квадратическое отклонение найдем соответственно по формулам

$$x^\ast = {\displaystyle 1\over\displaystyle n}\sum\limits_{i... ...isplaystyle 1\over\displaystyle 50}( - 10 + 15 + 30 + 15) = 1,$$

$$s = \sqrt {{\displaystyle 1\over\displaystyle n - 1}\sum\lim... ...0 + ( - 1)^2 \cdot 5 + 1 \cdot 15 + 2^2 \cdot 5} \approx 1,28.$$

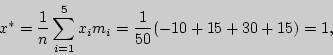
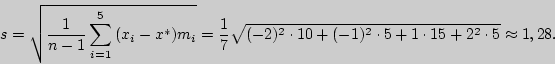
Пользуясь таблицей приложения 4, по $\alpha = 0,95$ и $n = 50$ находим $t_{\alpha } = 2,01$.

Найдем искомый доверительный интервал:

$$x^\ast - t_\alpha {\displaystyle s\over\displaystyle \sqrt n... ...^\ast + t_\alpha {\displaystyle s\over\displaystyle \sqrt n },$$

подставляя $х^{\ast } = 1$, $t_{\alpha } = 2,01$, $s \approx 1,28$, $n = 50$, получим $0,64 < a < 1,36$.

Пример 168. Результаты исследования длительности оборота (в днях) оборотных средств торговых фирм города Ярославля представлены в группированном виде:

$t_{i}$ - $t_{i + 1}$	24 - 32	32 - 40	40 - 48	48 - 56	56 - 64	64 - 72	72 - 80
$m_{i}$	2	4	10	15	11	5	3

Построить доверительный интервал с надежностью $0,99$ для средней длительности оборотных средств торговых фирм города.

Решение. Найдем выборочную среднюю длительности оборотных средств.

$$t^\ast = {\displaystyle 1\over\displaystyle 50}(28 \cdot 2 +... ... 52 \cdot 15 + 60 \cdot 11 + 68 \cdot 5 + 76 \cdot 3) = 52,96.$$

Для упрощения вычисления исправленного среднеквадратического отклонения выберем приближенное значение $t^\ast \approx 53$. Тогда

$\begin{array}{l} s = \sqrt {{\displaystyle 1\over\displaystyle 49}\left[ {(28 ... ...\displaystyle 1\over\displaystyle 7}\sqrt {6482} \approx 11,5. \\ \end{array}$

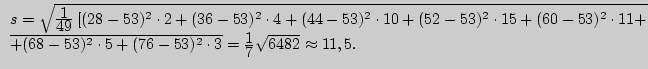
В приложении 4 по $n = 50$ и $\alpha =0,99$ находим $t_{\alpha } = 2,68$ , а следовательно, и доверительный интервал

$$52,96 - 2,68 \cdot {\displaystyle 11,5\over\displaystyle \sq... ... 2,68 \cdot {\displaystyle 11,5\over\displaystyle \sqrt {50} }$$

или $48,6 < a < 57,32$.

Рассматривая $n$ независимых испытаний, можно оценить вероятность $p$ по относительной частоте.

Пример 169. Сколько раз надо подбросить монету, чтобы с вероятностью $0,9$ можно было ожидать, что относительная частота появления "герба" отклонится от вероятности этого события по абсолютной величине не более чем на $0,05$?

Решение. По условию $\alpha = 0,95$, $p=1/2$, $\varepsilon = 0,1$.

Тогда $\alpha = P\left\{ {\left\vert {{\displaystyle m\over\displaystyle n} - {\displa... ...over\displaystyle \textstyle{1 \over 2} \cdot \textstyle{1 \over 2}}} } \right)$

$$2\Phi\left( {0,2\sqrt n } \right) \approx 0,95 \quad\mbox{и}\quad \Phi\left( {0,2\sqrt n } \right) \approx 0,475.$$

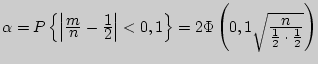
Из таблицы значений функции Лапласа находим, что $0,2\sqrt{n}\approx 2$, откуда $n \approx 100$.

Точечные оценки неизвестных параметров распределения можно находить по методу наибольшего правдоподобия, предложенному Р. Фишером.

Пример 170. Найти методом наибольшего правдоподобия оценку параметра $p$ биномиального распределения

$$P_n (k) = C_n^k \cdot p^k \cdot (1 - p)^{n - k},$$

если в $n_{1}$ независимых испытаниях событие $А$ появилось $m_{1}$ раз и в $n_{2}$ независимых испытаниях событие $A$ появилось $m_{2}$ раз.

Решение. Составим функцию правдоподобия:

$$L = P_{n_1 } (m_1 ) \cdot P_{n_2 } (m_2 ) = C_{n_1 }^{m_1 } ... ...p^{m_1 + m_2 }(1 - p)^{\left[ {(n1 + n2) - (m1 + m2)} \right]}$$

Найдем логарифмическую функцию правдоподобия:

$$\ln L = \ln \left( {C_{n_1 }^{m_1 } \cdot C_{n_2 }^{m_2 } } ... ...ln p + \left[ {(n_1 + n_2 ) - (m_1 + m_2 )} \right]\ln (1 - p)$$

Вычислим первую производную по $p$:

$${\displaystyle d\ln L\over\displaystyle dp} = {\displaystyle... ...laystyle (n_1 + n_2 ) - (m_1 + m_2 )\over\displaystyle 1 - p}.$$

Запишем уравнение правдоподобия, для чего приравняем первую производную нулю:

$${\displaystyle m_1 + m_2 \over\displaystyle p} - {\displaystyle (n_1 + n_2 ) - (m_1 + m_2 )\over\displaystyle 1 - p} = 0.$$

Решив полученное уравнение относительно $p$, найдем критическую точку:

$$p = {\displaystyle m_1 + m_2 \over\displaystyle n_1 + n_2 },$$

в которой производная отрицательна. Следовательно, $p = {\displaystyle m_1 + m_2 \over\displaystyle n_1 + n_2 }$ - точка максимума и, значит, ее надо принять в качестве наибольшего правдоподобия неизвестной вероятности $p$ биномиального распределения.

Вопросы для самоконтроля

1. Какая оценка называется точечной?
2. Какие точечные оценки генеральных числовых характеристик вы знаете?
3. Чем определяется интервальная оценка?
4. Надежность оценки и другое ее название.
5. На чем основано нахождение доверительного интервала для оценки математического ожидания?
6. Каким образом оценивают истинное значение измеряемой величины?
7. Точечная и интервальная оценка вероятности биномиального распределения.
8. В чем суть метода наибольшего правдоподобия?

Задачи

I 331. Игральная кость подбрасывается 300 раз. Какова вероятность того, что относительная частота появления шести очков на верхней грани кости отклонится от вероятности появления события в одном испытании по абсолютной величине не более чем на 0,05?

332. Сколько раз надо подбросить монету, чтобы с вероятностью 0,95 можно было ожидать, что относительная частота появления "герба" отклонится от вероятности этого события по абсолютной величине не более чем на 0,1?

333. Случайная величина $Х$ имеет нормальное распределение с известным средним квадратическим отклонением $\sigma = 1$. Найдите доверительные интервалы для оценки неизвестного математического ожидания $а$ по выборочным средним $х^{\ast } = 3,4$, если объем выборки $n = 49$ и задана надежность оценки $\gamma = 0,9$.

334. Исследовалось время безотказной работы 50 лазерных принтеров. Из априорных наблюдений известно, что среднее квадратическое отклонение времени безотказной работы $\sigma = 16$ч. По результатам исследований получено среднее время безотказной работы $x^{\ast }=1000$ч. Постройте 90%-й доверительный интервал для среднего времени безотказной работы.

335. Количественный признак $X$ генеральной совокупности распределен нормально. По выборке объема $n = 25$ найдено "исправленное" среднее квадратическое отклонение $S = 0,9$. Найдите доверительный интервал, покрывающий генеральное среднее квадратическое отклонение $\sigma$ с надежностью $0,95$.

336. Произведено 16 измерений одним прибором некоторой физической величины, причем исправленное среднее квадратическое отклонение $S$ случайных ошибок измерений оказалось равным 0,7. Найдите интервал ошибок прибора с надежностью 0,99. Предполагается, что ошибки измерений распределены нормально.

II 337. Время (в минутах) обслуживания клиентов в железнодорожной кассе представлено выборкой: 2,0; 1,5; 1,0; 1,0; 1,25; 3,5; 3,0; 3,0; 3.75; 3,7; 4,0; 6,0; 7,0; 1,5; 8,0; 3,5; 5,0; 3,5; 14,0; 12,0; 15,1; 18,0; 18,5; 17,0. Определите процент клиентов, время обслуживания которых более 12 минут и менее 5 минут.

338. Из генеральной совокупности извлечена выборка объема $n = 16$:

$х_{i}$	-0,4	-0,2	-0,1	0	0,2	0,5	0,7	1	1,2	1,6
$m_{i}$	1	3	2	1	1	1	2	1	2	2

Оцените с надежностью 0,9 математическое ожидание $a$ нормально распределенного признака генеральной совокупности с помощью доверительного интервала.

III 339. Результаты исследования длительности оборота оборотных средств торговых фирм города (в днях) представлены в группированном виде:

$t_i - t_{i+1}$	24-33	33-42	42-51	51-60	60-69	69-78	78-87
$m_{i}$	1	4	9	18	10	6	2

Постройте доверительный интервал с надежностью 0,95 для средней длительности оборотных средств торговых фирм города при условии, что среднее квадратическое отклонение $\sigma$ неизвестно (известно и равно 10 дням).

340. Найти методом наибольшего правдоподобия оценку параметра $\lambda$ распределения Пуассона

$$P_m \{X = x_i \} = {\displaystyle \lambda ^{x_i } \cdot e^{ - \lambda }\over\displaystyle x_i !}.$$

Далее: §35. Выборочный коэффициент корреляции Вверх: Глава V. Математическая статистика Назад: §33. Выборочные характеристики вариационного