Далее: §36. Ранговая корреляция Вверх: Глава V. Математическая статистика Назад: §34. Доверительный интервал

§35. Выборочный коэффициент корреляции

Понятие корреляции является одним из основных понятий теории вероятностей и математической статистики, оно было введено Гальтоном и Пирсоном.

Закон природы или общественного развития может быть представлен описанием совокупности взаимосвязей. Если эти зависимости стохастичны, а анализ осуществляется по выборке из генеральной совокупности, то данная область исследования относится к задачам стохастического исследования зависимостей, которые включают в себя корреляционный, регрессионный, дисперсионный и ковариационный анализы. В данном разделе рассмотрена теснота статистической связи между анализируемыми переменными, т.е. задачи корреляционного анализа.

В качестве измерителей степени тесноты парных связей между количественными переменными используются коэффициент корреляции (или то же самое "коэффициент корреляции Пирсона") и корреляционное отношение.

Пусть при проведении некоторого опыта наблюдаются две случайные величины $X$ и $Y$, причем одно и то же значение $x$ встречается $n_{х}$ раз, $у - n_{у}$ раз, одна и та же пара чисел ($х, у)$ наблюдается $n_{ху}$ раз. Все данные записываются в виде таблицы, которую называют корреляционной.

Выборочная ковариация $k(X, Y)$ величин $X$ и $Y$ определяется формулой

$$k(X,Y) = {\displaystyle 1\over\displaystyle n}\sum {(x_i - x^\ast )(y_i - y^\ast )n_{xy} } ,$$

где $n = \sum n_{ху}$, а $х^{\ast }$, $y^{\ast}$ - выборочные средние величин $Х$ и $Y$. При небольшом количестве экспериментальных данных $k(X, Y)$ удобно находить как полный вес ковариационного графа:

Рис. 101

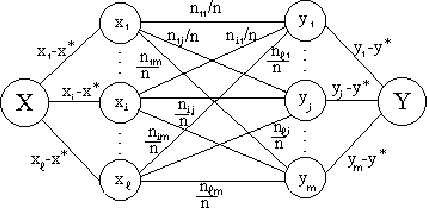
Выборочный коэффициент корреляции находится по формуле

$$r(X,Y) = {\displaystyle k(X,Y)\over\displaystyle \sigma _х^\... ...ast \over\displaystyle n\sigma _х^\ast \cdot \sigma _у^\ast },$$

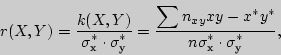
где $\sigma _х^\ast , \sigma _у^\ast$ - выборочные средние квадратические отклонения величин $Х$ и $Y$.

Выборочный коэффициент корреляции $r(X,Y)$ показывает тесноту линейной связи между $X$ и $Y$: чем ближе $\vert r(X, Y)\vert$ к единице, тем сильнее линейная связь между $Х$ и $Y$.

Пример 171. Среднемесячная заработная плата (тыс. руб.) в Ярославской области в 2001-2002 годах составила по отраслям:

отрасль	ЖКХ	здравоохранение	наука	образование	транспорт	промышленность
2001 год	2	1,5	2,7	1,3	3,2	3,2
2002 год	3	2,8	3,6	2,4	4,9	4,5

Найдите выборочный коэффициент корреляции для заработной платы в указанные годы.

Решение. 1). Найдем выборочные средние

$$х^\ast = {\displaystyle 1\over\displaystyle 6}(2 + 1,5 + 2,7 + 1,3 + 3,2 + 3,2) \approx 2,3; \qquad у^\ast \approx 3,5.$$

2). Вычислим выборочную ковариацию

$$\begin{array}{l} k(X,Y) = {\displaystyle 1\over\displaystyl... ...3) \cdot (4,5 - \left. {3,5)} \right] = 0,668. \\ \end{array}$$

3). Найдем выборочные средние квадратические отклонения:

$$\begin{array}{l} D_х^\ast = {\displaystyle 1\over\displayst... ...; \\ D_у^\ast = 0,82; \sigma _у^\ast = 0,91. \\ \end{array}$$

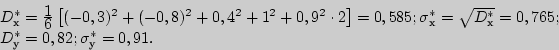
4). Вычислим теперь выборочный коэффициент корреляции

$$r(X,Y) = {\displaystyle k(X,Y)\over\displaystyle \sigma _х^\... ...ystyle 0,668\over\displaystyle 0,765 \cdot 0,91} \approx 0,96.$$

Поскольку $r(X,Y)$ достаточно близко к $1$, то между заработной платой по отраслям в 2001 и 2002 годах существовала почти линейная зависимость (зарплата в 2002 году по каждой отрасли увеличилась примерно в 1,5 раза).

Пример 172. В выпускном классе проводились контрольные работы по физике и математике, которые дали следующие результаты:

Оценки по математике	2	3	4	5
Оценки по физике
2 3 4 5	1 1 - -	2 4 1 1	1 2 3 3	- - 4 2

Найдите выборочный коэффициент корреляции оценок контрольных работ по физике и математике.

Решение. В этом случае удобно начать с построения ковариационного графа, вычислив предварительно выборочные средние.

$$х^\ast = 2 \cdot 0,16 + 3 \cdot 0,28 + 4 \cdot 0,32 + 5 \cdot 0,24 = 3,64 \approx 3,6; у^\ast = 3,76 \approx 3,8.$$

Рис. 102

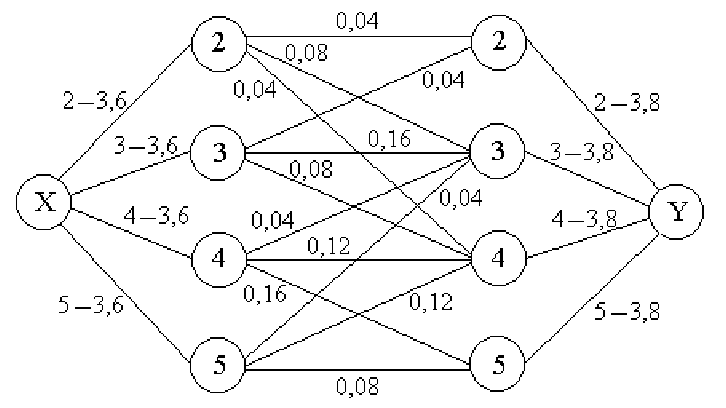
Выборочную ковариацию находим как вес всего ковариационного графа:

$$\begin{array}{l} k(X,Y) = ( - 1,6) \cdot 0,04 \cdot ( - 1,8... ... \cdot 0,2 + 1,4 \cdot 0,08 \cdot 1,2 = 0,512. \\ \end{array}$$

По графу можно вычислить и выборочные дисперсии

$$\begin{array}{l} D_х^\ast = ( - 1,6)^2 \cdot (0,04 + 0,08 +... ...t \approx 1,016, \sigma _у^\ast \approx 0,908. \\ \end{array}$$

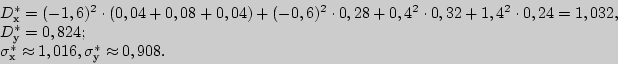
Следовательно, 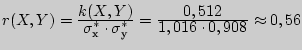$r(X,Y) = {\displaystyle k(X,Y)\over\displaystyle \sigma _х^\ast \cdot \sigma _у^\ast } = {\displaystyle 0,512\over\displaystyle 1,016 \cdot 0,908} \approx 0,56$ и можно утверждать, что между оценками тех контрольных работ по физике и математике существует средней тесноты линейная прямая связь.

Корреляционной зависимостью $Y$ от $Х$ называют функциональную зависимость условной средней $у_х^\ast$ от $х$.

$у_х^\ast = f(x)$ представляет уравнение регрессии $Y$ на $Х$, а $x_y^\ast = \varphi (y)$ - уравнение регрессии $Х$ на $Y$.

Корреляционная зависимость может быть линейной и криволинейной. В случае линейной корреляционной зависимости выборочное уравнение прямой линии регрессии $Y$ на $Х$ имеет вид:

$$у_х^\ast - y^\ast = {\displaystyle k(X,Y)\over\displaystyle D_х^\ast }(x - x^\ast ).$$

Параметры $a$ и $b$ уравнения прямой $у_х^\ast = ax + b$ линии регрессии $Y$ на $Х$ можно находить по методу наименьших квадратов из системы уравнений

$$\left\{ {\begin{array}{l} n(x^\ast )^2a + nx^\ast b = \sum {n_{xy} xy} \\ x^\ast a + b = y^\ast \\ \end{array}} \right.$$

Пример 173. Построить прямую регрессии мировых рекордов по прыжкам с шестом от соответствующего года, если нам известна динамика результатов в ХХ веке.

1912 г. 1936 г. 1972 г. 1980 г. 1988 г. 1994 г.

Стокгольм, Берлин, Мюнхен, Москва, Сеул, Сетриере

Гарри Бебкок (США) Эрл Мидоуз (США) Волфганг Нордвик (ГДР) Владислав Казакевич (Польша) Сергей Бубка (СССР) Сергей Бубка (Украина)

3,95 4,35 5,50 5,78 5,90 6,14

Решение. 1). Запишем в таблицу соответствие результатов некоторых мировых рекордов по прыжкам с шестом и годы их установления в ХХ веке.

$Х$ = {год рекорда}	(19)12	36	72	80	88	94
$Y$ = {высота рекорда}	395	435	550	578	590	614

2). $х^\ast = 64; \quad у^\ast = {\displaystyle 1\over\displaystyle 6}(395 + 435 + 550 + 578 + 590 + 614) = 527$(см.)

3). $k(X,Y) = {\displaystyle 1\over\displaystyle 6}\left[ {( - 52) \cdot ( - 132) + ... ...) + 8 \cdot 23 + 16 \cdot 51 + 24 \cdot 63 + 30 \cdot 87} \right] \approx 2427;$

4). $D_х^\ast = {\displaystyle 1\over\displaystyle 6}\left[ {( - 52)^2 + ( - 28)^2 + 8^2 + 16^2 + 24^2 + 30^2} \right] \approx 880;$

5). Искомое уравнение прямой регрессии выглядит следующим образом

$$y_x^\ast - 527 = {\displaystyle 2427\over\displaystyle 880}(x - 64),$$

или $y_x^\ast = 2.75x + 351.$

По полученной прямой регрессии можно на вероятностном языке предсказывать уровень мировых рекордов по прыжкам с шестом, так, в 2010 году
($х$ = 110) получаем ожидаемый прыжок на высоту примерно в 6 м 53 см. (поживем - увидим!)

В том случае, когда исследуется связь между несколькими признаками, то корреляцию называют множественной и она задается всеми коэффициентами парных корреляций, которые записываются в корреляционную матрицу.

Пример 174. Найти корреляционную матрицу зависимости суммы двоеборья, результатов в толчке и рывке, веса спортсмена и его возраста для пяти весовых категорий тяжелоатлетов.

№ категории	$x_{1}$ Двоеборье	$x_{2}$ Рывок	$x_{3}$ Толчок	$x_{4}$ Вес атлета	$x_{5}$ Возраст
1	400	180	220	80	24
2	420	195	225	90	27
3	440	200	240	100	21
4	435	195	240	110	26
5	465	205	260	130	22

Решение. 1). $х_1^\ast = 432, \quad х_2^\ast = 195, \quad х_3^\ast = 237, \quad х_4^\ast = 102, \quad х_5^\ast = 24.$

2). Составим таблицу разностей $x_i - x_i^\ast$ и их квадратов

№ категории	${x_1 - x_1^\ast } \mathord{\left/ {\vphantom {{x_1 - x_1^\ast } {(x_1 - x_1^\ast )^2}}} \right. \kern-\nulldelimiterspace} {(x_1 - x_1^\ast )^2}$	${x_2 - x_2^\ast } \mathord{\left/ {\vphantom {{x_2 - x_2^\ast } {(x_2 - x_2^\ast )^2}}} \right. \kern-\nulldelimiterspace} {(x_2 - x_2^\ast )^2}$	${x_3 - x_3^\ast } \mathord{\left/ {\vphantom {{x_3 - x_3^\ast } {(x_3 - x_3^\ast )^2}}} \right. \kern-\nulldelimiterspace} {(x_3 - x_3^\ast )^2}$	${x_4 - x_4^\ast } \mathord{\left/ {\vphantom {{x_4 - x_4^\ast } {(x_4 - x_4^\ast )^2}}} \right. \kern-\nulldelimiterspace} {(x_4 - x_4^\ast )^2}$	${x_5 - x_5^\ast } \mathord{\left/ {\vphantom {{x_5 - x_5^\ast } {(x_5 - x_5^\ast )^2}}} \right. \kern-\nulldelimiterspace} {(x_5 - x_5^\ast )^2}$
1	-32 / 1024	-15 / 225	-17 / 289	-22 / 484	0 / 0
2	-12 / 144	0 / 0	-12 / 144	-12 / 144	3 / 9
3	8 / 64	5 / 25	3 / 9	-2 / 4	-3 / 9
4	3 / 9	0 / 0	3 / 9	8 / 64	2 / 4
5	33 / 1089	10 / 100	23 / 529	28 / 784	-2 / 4

3). Найдем ковариации $k(x_{i}, x_{j})=k_{ij}$.

$$k_{12} = {\displaystyle 1\over\displaystyle 5}\left[ {( - 32... ...\rm н}{\rm а}{\rm л}{\rm о}{\rm г}{\rm и}{\rm ч}{\rm н}{\rm о}$$

$k_{13 }= 296, k_{14 }= 356, k_{15 }= -24$,

$k_{23 }= 100, k_{24 }= 120, k_{25 }= -7$,

$k_{34 }= 236, k_{35 }= -17, k_{45 }= -14$.

4). Вычислим дисперсии и по ним - средние квадратические отклонения

$$D_{х_1 }^\ast = {\displaystyle 1\over\displaystyle 5}(1024 +... ...d \sigma _{х_1 }^\ast = + \sqrt {D_{х_1 }^\ast } \approx 21,6;$$

$$D^\ast [X_2 ] = 70\quad\mbox{и} \quad \sigma _{х_2 }^\ast \a... ...{х_3 }^\ast = 196\quad\mbox{и} \quad \sigma _{х_3 }^\ast = 14;$$

$$D_{х_4 }^\ast = 296\quad\mbox{и} \quad \sigma _{х_4 }^\ast \... ...\ast = 5,2\quad\mbox{и} \quad \sigma _{х_5 }^\ast \approx 2,3.$$

5). Найдем выборочные коэффициенты парной корреляции

$$r_{12} = {\displaystyle k_{12} \over\displaystyle \sigma _{х... ...playstyle 170\over\displaystyle 21,6 \cdot 8,37} \approx 0,94;$$

$r_{13 } \approx 0,98; r_{14 } \approx 0,96; r_{15 } \approx -0,48$;

$r_{23 } \approx 0,85; r_{24 } \approx 0,83; r_{25 } \approx -0,36$;

$r_{34 } \approx 0,98; r_{35 } \approx -0,52; r_{45 } \approx -0,35$.

6). Запишем полученные результаты в виде корреляционной матрицы $(\mbox{\boldmath$r$})$, учитывая, что $r_{ii} = 1$, a $r_{ij}= r_{ji}$:

$$\left( {\rm {\bf r}} \right) = \left[ {{\begin{array}{*{20}c... ...\hfill & \hfill & \hfill & 1 \hfill \\ \end{array} }} \right]$$

Определите, какие показатели имеют наибольшую (наименьшую) прямую связь.

Для оценки тесноты нелинейной корреляционной связи вводят выборочные корреляционные отношения. Выборочным корреляционным отношением $Y$ к $Х$ называют отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака $Y$:

$\eta_{ух} =\sigma _{межгр}/ \sigma_{общ}$, или в других обозначениях

$$\eta _{yx} = {\sigma _{y\ast _x }^{}} \mathord{\left/ {\vpha... ...\ast }}} \right. \kern-\nulldelimiterspace} {\sigma _y^\ast }.$$

$$0 \le \eta \le 1,$$

и если $\eta = 0$, то признак $Y$ c признаком $Х$ корреляционной зависимостью не связан, а если $\eta = 1$, то признак $Y$ связан c признаком $Х$ функциональной зависимостью.

Пример 175. Найти выборочное корреляционное отношение между себестоимостью зерна и урожайностью зерновых по данным 80 хозяйств области.

Урожайность зерновых, ц/га Х	Себестоимость 1 ц зерна, руб. Y				Число хозяйств	Средняя себестоимость 1 ц зерна по группам $y_j^\ast$
	до 200 $у_{1 }= 180$	200-240 $у_{2} = 220$	240-280 $у_{3 }= 260$	свыше 280 $у_{4 }= 300$
до 15	-	-	-	2	2	300
15 - 17	-	1	2	3	6	273,3
17 - 19	-	-	7	1	8	265
19 - 21	-	8	8	-	16	240
21 - 23	2	20	12	-	34	231,8
23 - 25	1	8	1	-	10	220
свыше 25	3	1	-	-	4	190
Число хоз-в	6	38	30	6	80	$у^{\ast } = 238$

Решение. 1). Найдем выборочную среднюю себестоимости:

$$у^\ast = {\displaystyle 1\over\displaystyle 80}(6 \cdot 180 + 38 \cdot 220 + 30 \cdot 260 + 6 \cdot 300) = 238.$$

2). Найдем общее среднее квадратическое отклонение:

$\sigma _у^\ast = \sqrt {\textstyle{1 \over {80}}\left[ {6 \cdot (180 - 238)^2 +... ...8)^2 + 30 \cdot (260 - 238)^2 + 6 \cdot (300 - 238)^2} \right]} \approx 29,6.3)$. Найдем межгрупповое среднее квадратическое отклонение:

$$\begin{array}{l} \sigma _{у\ast _х } = \sqrt {\textstyle{1 ... ...(190 - \left. {238)^2} \right]} \approx 20,86. \\ \end{array}$$

4). Вычислим теперь искомое корреляционное отношение:

$$\eta _{yx} = {\sigma _{y\ast _x }^{} } \mathord{\left/ {\vph... ... } = {\displaystyle 20,86\over\displaystyle 29,6} \approx 0,7.$$

Полученное значение $\eta$ = 0,7 характеризует тесноту связи выше средней.

Вопросы для самоконтроля

1. Какой граф называется ковариационным?
2. Как можно вычислять выборочную ковариацию?
3. О чем судят по выборочному коэффициенту корреляции?
4. Что такое корреляционная зависимость?
5. Простейший вид корреляционной зависимости.
6. Какой метод нахождения линии регрессии вы знаете?
7. Расскажите о методике вычисления выборочного коэффициента корреляции.
8. Назовите свойства выборочного корреляционного отношения.

Задачи

I 341. Итоги аттестации педагогических работников Ярославской области на квалификационные категории за 1998 - 2002 годы представлены в таблице:

Годы	1998	1999	2000	2001	2002
ВК	433	494	638	634	1287
${\rm I}{\rm к}{\rm а}{\rm т} \quad .$	1371	1512	2166	2170	3004

Найдите выборочный коэффициент корреляции между первой и высшей категориями.

342. О ходе уборки зерновых в 20 хозяйствах области, отобранных случайным образом, представлены следующие данные ($Х$ - скошено тыс. га, $Y$ - обмолочено тыс. га):

$X$	4	3.5	3.5	3.5	3.5	3	3.5	3.5	4	4	3	3	3	4	4	3.5	3	4	3	4
$Y$	3	2.5	2	2.5	2	2.5	3	2	3	2.5	2	2.5	2	2.5	3	3	2.5	3	2	2.5

Сгруппируйте данные в корреляционную таблицу. Постройте ковариационный граф и найдите ковариацию.

343. Найдите уравнение прямой линии регрессии $Y$ на $Х$ по данным $n = 20$ наблюдений:

$Y$ $X$	2	4
1	8	2
3	4	6

344. Известна реальная начисленная среднемесячная заработная плата по кварталам 2002 г., в % к предыдущему периоду:

Квартал	1	2	3	4
%	86	97	105	102

Найдите уравнение регрессии $у=ax+b$ методом наименьших квадратов.

345. Средняя стоимость (в тыс. руб.) $1\mbox{м}^{2}$ жилых домов по городу Ярославлю за последние шесть лет составила:

Годы	1	2	3	4	5	6
Стоимость	5,6	6	6,5	11,7	12,4	16

Выразите эти данные по прямой $у=ах+b$ методом наименьших квадратов.

346. Найдите прямую регрессии цены на золото на мировом рынке за последние десять лет по данным World Gold Conneil.

Год	1993	1995	1997	1999	2001	2003
цена на золото ($ за 1 унцию)	360	395	315	290	260	305

II 347. Найдите степень тесноты множественной статистической связи между стоимостью квартир ($Х$ в тыс. руб.), площадью ($Y$ в м$^{2})$ и их удаленностью от областного центра ($Z$ в км) по приведенным результатам исследования.

$X$	560	700	290	690	250	600	690
$Y$	44	69	27	78	30	48	54
$Z$	74	47	92	48	93	72	71

348. Количество дошкольных учреждений системы образования Ярославской области за последние пять лет изменялось следующим образом:

Годы ($Х)$	1	2	3	4	5
Кол-во ($Y)$ дошк. учрежд.	480	520	520	480	490

Полагая, что $Х$ и $Y$ связаны зависимостью $у=ах^{2}+bх+с$, найдите коэффициенты $а, b$и$с$ методом наименьших квадратов.

III 349. Найдите выборочные уравнения прямых линий регрессии $Y$ на $Х, Х$ на $Y$ по данным, приведенным в корреляционной таблице:

$Y$ $Х$	10	15	20	25	30	$nх$
2 12 22 32 42	2 - - - -	3 4 - - -	- 5 16 3 -	- - 2 6 1	- - 4 2 2	5 9 22 11 3
$nу$	2	7	24	9	8	$n = 50$

350. Найдите выборочное уравнение регрессии $ух^{\ast }=Ах^{2}+Вх+С$ и выборочное корреляционное отношение по данным, приведенным в корреляционной таблице:

$Y$ $Х$	0	4	5	$nх$
1	30	5	1	36
20	-	14	-	14
50	-	5	45	50
$nу$	30	24	46	$n = 100$

Далее: §36. Ранговая корреляция Вверх: Глава V. Математическая статистика Назад: §34. Доверительный интервал