Далее: Указатель обозначений Вверх: Глава V. Математическая статистика Назад: §39. Математическая статистика в

§40. Статистические методы в педагогике

С помощью математической статистики выявляется обоснованность заключений педагогических исследований. Целью экспериментального исследования является, как правило, проверка эффективности того или иного педагогического подхода к решению поставленной в исследовании задачи. Педагогический эксперимент традиционно проводится в три этапа.

На первом (констатирующем) этапе проводится анализ педагогических условий, сложившихся в современной практике на обозначенной проблеме, и диагностическое исследование участников. Выделяются контрольные и экспериментальные группы примерно равной численности и уровня подготовленности. Результаты констатирующего этапа должны свидетельствовать о нерешенности (искомой осознанности, недостаточном осмыслении) проблемы.

На втором (формирующем) этапе эксперимента реализуются обозначенные педагогические условия. В рамках реализации педагогических, учебно-методических условий студентам экспериментальной группы предлагаются программы по формированию умений и навыков умения работы с информацией, организации учебного процесса и самостоятельной работы, их контроля.

На третьем (контрольном) этапе проводится повторное диагностическое исследование качества обучения в контрольной и экспериментальной группах. Полученные результаты сопоставляются с данными констатирующего этапа эксперимента, делаются выводы. Особое внимание уделяется обоснованности выводов при использовании того или иного критерия достоверности на заданном уровне значимости.

Принцип отбора критериев в данном параграфе - простота и практичность. Большинство методов построены на понятных для педагогов преобразованиях.

Алгоритм применения критерия $\mbox{\boldmath$Q$}$ Розенбаума для оценки между двумя выборками по уровню признака

  1. Проверить, выполняются ли ограничения: $n_{1}$, $n_{2} \ge 11$, $n_{1} \approx n_{2}$.
  2. Упорядочить значения отдельно в каждой выборке по степени возрастания признака. Считать выборкой 1 ту, значения в которой предположительно больше.
  3. Определить максимальное значение в выборке 2.
  4. Подсчитать количество $S_{1}$ значений в выборке 1, которые больше максимальных значений в выборке 2.
  5. Определить минимальное значение в выборке 1.
  6. Подсчитать количество $S_{2}$ значений в выборке 2, которые меньше минимального значения выборки 1.
  7. Подсчитать эмпирическое значение $Q_{эмп}= S_{1}+S_{2}$.
  8. По таблице приложения 9 определить критические значения $Q_{кр}$ для данных $n_{1}$ и $n_{2}$. Если $Q_{эмп} \ge Q_{кр}$, то $H_{0}$ отвергается.

Пример 196. Можно ли считать эффективными результаты педагогического эксперимента по изменению показателей психологической защищенности старших подростком до и после эксперимента:

Показатели

психологич

еской

защищенно

сти

 Младшие подр.

(сред. значен.)

 Старшие подр.

(сред. значен.)

 Педагоги

(сред. значен.)
  До После До После До После
От публичного унижения учеников

учителей

 2,4

2,4

 2,6

2,8

 3,1

2,9

 3,9

3,8

 2,6

2,7

 3,5

3,7
От оскорблений учеников

учителей

 2,1

2,7

 2,2

2,8

 2,8

3,0

 3,8

3,1

 2,4

2,7

 3,0

3,7
От высмеиваний учеников

учителей

 2,2

2,7

 2,4

2,9

 2,6

3,0

 3,8

4,0

 2,6

2,8

 2,6

2,8
От угроз учеников

учителей

 2,5

2,7

 2,8

3,1

 3,2

3,2

 4,2

3,2

 2,8

2,9

 3,7

3,9
От обзываний учеников

учителей

 2,2

2,5

 2,3

2,9

 2,4

3,0

 3,7

3,8

 2,5

2,9

 3,5

3,9
От того, что заставят делать

против желания ученики

учителя

 2,7

2,1

 3,0

2,5

 3,2

2,1

 4,1

2,5

 2,7

2,4

 4,0

3,6
От игнорирования учеников

учителей

 2,4

2,6

 2,8

2,7

 2,6

2,5

 3,6

3,8

 2,6

2,6

 2,6

2,6
От неуважит. отношения учеников

учителей

 2,2

2,4

 2,6

2,8

 2,6

2,8

 3,6

2,9

 2,4

2,6

 3,6

3,7
От недоброжелательного

отношения учеников

учителей

 2,2

2,4

 2,4

2,7

 2,6

2,6

 3,7

2,8

 2,3

2,5

 3,6

2,7

Решение. 1). $n_{1} = n_{2}= 18$.

2). Выборкой 1 считаем средние значения защищенности после эксперимента.

3). Максимальное значение в выборке до эксперимента равно 3,2.

4). $S_{1}=12$.

5). Минимальное значение в выборке 1 равно 2,5.

6). $S_{2} = 2$.

7). $Q_{эмп}= S_{1}+ S_{2}=12 + 2 = 14$.

8). По приложению 9 при $n_{1}=n_{2}=$18 и $p=0,01$ находим $Q_{{кр}} = 9$.

Поскольку $Q_{эмп}=14>Q_{кр}=9$, то $H_{0}$ отклоняется и можно считать эффективными результаты эксперимента.

Алгоритм применения критерия $\mbox{\boldmath$H$}$ Крускала - Уоллиса для оценки различий между несколькими выборками по уровню признака

  1. Перенести все показатели испытуемых на индивидуальные карточки.
  2. Пометить карточки испытуемых каждой группы своим цветом.
  3. Разложить все карточки в единый ряд по степени нарастания признака.
  4. Проранжировать значения на карточках, приписывая меньшему значению меньший ранг. Написать на каждой карточке ее ранг.
  5. Вновь разложить карточки по группам, ориентируясь на цвет.
  6. Подсчитать суммы рангов отдельно по каждой группе. Проверить совпадение общей суммы рангов с расчетной.
  7. Подсчитать значение критерия $Н_{эмп}$ по формуле:

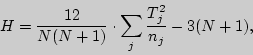
    \begin{displaymath} H = {\displaystyle 12\over\displaystyle N(N + 1)} \cdot \sum... ..._j {{\displaystyle T_j ^2\over\displaystyle n_j }} - 3(N + 1), \end{displaymath}

    где $N$ - общее количество испытуемых, $Т_{j}$ - сумма рангов в $j$-й группе, состоящей из $n_{j}$ испытуемых.
  8. а) При количестве группы $с=$3 или количестве испытуемых $n_{1},_{ }n_{2}, n_{3 }$$ \le $ 5 определить критические значения по таблице.

    б) При количестве $с>3$ или количестве испытуемых $n_{1},_{ }n_{2}, n_{3 }>5$ определить критические значения $\chi^{2}$ по приложению 5.

    Если $Н_{эмп} \ge Н_{кр}$, то $Н_{0}$ отвергается.

Пример 197. Одинаковы ли воздействия педагогического эксперимента на младших и старших подростков, а также на учителей под воздействием учеников по показателям психологической защищенности после эксперимента из предыдущего примера?

Решение. Составим таблицу получившихся рангов по трем группам и их суммы:

                    $\sum $
младшие подр. 6,5 1 3,5 9,5 2 11,5 9,5 6,5 3,5 53,5
старшие подр. 24 22,5 22,5 27 20 26 16,5 16,5 20 195
педагоги 13,5 11,5 6,5 20 13,5 25 6,5 16,5 16,5 125,5
Проверка: $1 + 2 +\ldots + 27 = {1 + 27 \over 2} \cdot 27 = $ 378

Подсчитаем значения критерия


\begin{displaymath} Н_{эмп} = {\displaystyle 12\over\displaystyle N(N + 1)} \cdo... ...,5^2\over\displaystyle 9}} \right) - 3 \cdot 28 \approx 17,69. \end{displaymath}

Определим по приложению 5 критическое значение $\chi_{кр}^2 $ для уровня значимости $\alpha = 0,01$ и степеней свободы $k=3-1$. $\chi_{кр}^2(0,01; 2) = 9,21$.

Поскольку $Н_{эмп} = 17,69 > 9,21 = \chi _{кр}^2 $, то $Н_{0}$ отвергается, т.е. результаты воздействия эксперимента на младших и старших подростков и учителей различны.

Алгоритм применения критерия $\chi_r^2$ Фридмана для сопоставления трех и более показателей испытуемых

  1. Проранжировать индивидуальные значения каждого испытуемого, полученные им в 1-м, 2-м, 3-м и т. д. замерах.
  2. Просуммировать ранги, проверить совпадение общей суммы рангов с расчетной.
  3. Определить эмпирическое значение $\chi_r^2$ по формуле: $\chi_{r_{эмп}} = {\displaystyle 12\over\displaystyle n \cdot c\left( {c + 1} \right)}\sum {\mathop T\nolimits_j^2 } - 3n\left( {c + 1} \right)$,где $с$ - количество условий, $n$ - количество испытуемых, $T_j $- сумма рангов по каждому из условий.
  4. Определить уровни статистической значимости для $\chi_r^2$, для $с=3$, $n \le 9$ и $с=4$, $n\le4$ (по таблице).
  5. При большом количестве условий или испытуемых определить критические значения критерия $\chi_{кр}^2 $ при данном числе степеней свободы $\nu =c - 1$.

    Если $\chi_{r_{эмп}}^2 \ge \chi_{кр}^{2}$, то различия статистически достоверны.

    Критерий применяется для сопоставления показателей, измеренных в трех и более условиях на одной и той же выборке испытуемых.

Пример 198. Пять учащихся исследуются по четырем тестам. Являются ли результаты тестирования случайными?
  Баллы по тесту Ранг по баллам
№ А Б С Д А Б С Д
1

2

3

4

5

 3,6

3,8

3,3

3,8

4

 4,1

4.2

3,8

3,3

3,6

 2,9

3,7

3

3,4

1,9

 3,5

4,6

3,7

2,7

3,1

 2

3

3

1

1

 1

2

1

3

2

 4

4

4

2

4

 3

1

2

4

3
Сумма 10 9 18 13

2. $10 + 9 + 18 + 13 = 50 = 5 \cdot 10$.

3. $\chi_{r_{эмп}}^2 = {\displaystyle 12\over\displaystyle 5 \cdot 4 \cdot \left( {... ...^2 + 9^2 + 18^2 + 13^2} \right) - 3 \cdot 5 \cdot \left( {4 + 1} \right) = 5,88$

5. Для $3\left( { = с - 1} \right)$ степень свободы находим по таблице $\mathop х\nolimits_{кр}^2 = 7,815\left( {{\rm\rho } \le 0,05} \right)$.

Поскольку $\chi_{r_{эмп}}^2 = 5,88 < 7,82 = \chi_{кр}^2 $, то различия результатов тестирования достаточно случайны.

Алгоритм применения критерия Барлетта для оценки однородности дисперсий

  1. Вычислить выборочные дисперсии $D_j^\ast $ для каждой из $m$ выборок объемом $n_{j}.$
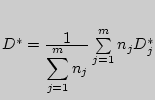  2. Вычислить $В = $2,3 $\left[ {\left( {\sum\limits_{j = 1}^m {n_j - m} } \right)\lg D^\ast - \sum\limits_{j = 1}^m {(n_j - 1)\lg D_j^\ast } } \right],$ где $D^\ast = {\displaystyle 1\over\displaystyle \sum\limits_{j = 1}^m {n_j } }\sum\limits_{j = 1}^m {n_j D_j^\ast } $.
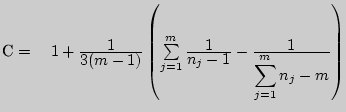  3. Вычислить $С = \quad 1 + {\displaystyle 1\over\displaystyle 3(m - 1)}\left( {\sum\limits_{... ...{\displaystyle 1\over\displaystyle \sum\limits_{j = 1}^m {n_j - m} }} } \right)$.
  4. Найти отношение $В/С$, которое распределено приблизительно по закону $\chi^{2}$ с $k = m -1$ степенями свободы при условии, что все $n_{j } \ge 5$.
  5. Гипотеза об однородности всех $D_j^\ast $ принимается, если $B/С\le \chi^{2}(\alpha, m -1)$, и отклоняется, если $B/С > \chi^{2}(\alpha, m -1)$.

Пример 199. Определить, изменяется ли дисперсия оценок при переходе от младших школьников к старшим, если ученики сельской школы получили следующие оценки по тесту "числовые ряды":

  6 кл. 7 кл. 8 кл. 9 кл. 10 кл. 11 кл.
Оценки

по

тесту

$(х_{ij})$

 9,5

12,0

14,0

12,5

10,0

14,5

15,0

9,0

20,0

12,5

14,0

11,5

13,0

14,0

13,0

 13,0

18,5

13,5

17,0

11,5

15,0

18,5

14,5

10,5

13,5

14,0

16,5

7,5

-

-

 18,5

14,0

15,0

11,5

15,0

14,5

19,0

18,0

10,0

14,5

18,0

13,0

14,5

19,0

-

 19,5

17,0

14,5

20,0

19,5

23,0

17,5

17,0

13,0

21,0

17,0

20,5

18,5

-

-

 18,0

23,5

16,5

22,0

19,0

15,5

25,0

21,0

21,0

20,5

20,0

16,5

-

-

-

 18,5

1,0

17,5

19,0

18,5

18,0

19,5

20,5

23,0

19,5

22,5

-

-

-

-
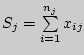$S_j = \sum\limits_{i = 1}^{n_j } {x_{ij} } $ 184,5 183,5 214 238 238,5 214,5
$n_{j}$ 15 13 14 13 12 11

Составим таблицу к расчету критерия Барлетта при неравных объемах выборок.

J

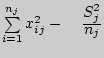$\sum\limits_{i = 1}^{n_j } {x_{i_j } ^2} $ ${\displaystyle S_j^2 \over\displaystyle n_j }$ $\sum\limits_{i = 1}^{n_j } {x_{ij}^2 } - \quad {\displaystyle S_j^2 \over\displaystyle n_j }$ $n_j - 1$ $D_j^\ast $ $ \lg D_j^\ast $ $(n_j - 1) \cdot \lg D_j^\ast $
1

2

3

4

5

6

$\sum $

 2621,3

2709,3

3390,3

4445,5

4833,3

4215,8

2269,4

2590,2

3271,1

4357,2

4740,2

4182,8

21410,9

 351,9

119,1

119,2

88,3

93,1

33,0

804,6

 14

12

13

12

11

10

72=m(n-1)

 25,14

9,93

9,17

7,36

8,46

3,30

63,62

 1,40

0,997

0,962

0,867

0,928

0,519

-

 19,6

11,964

12,506

10,404

10,208

5,19

69,872

Найдем общую выборочную дисперсию $D^{\ast }$ по указанной в критерии формуле:


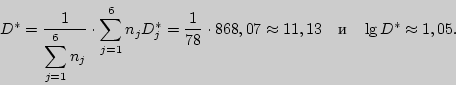
\begin{displaymath} D^\ast = {\displaystyle 1\over\displaystyle \sum\limits_{j =... ...8,07 \approx 11,13\quad\mbox{и} \quad \lg D^\ast \approx 1,05. \end{displaymath}

Вычислим $В = 2,3 \cdot \left[ {(\sum {n_j - m)\lg D^\ast } - \sum {(n_j - 1)\lg D_j^\ast... ...\cdot \left[ {(78 - 6) \cdot 1,05 - 69,872} \right] \approx 13,17 \quad\mbox{и}$


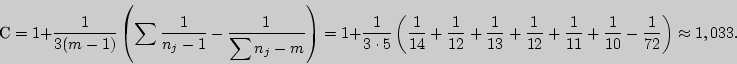
\begin{displaymath} С = 1 + {\displaystyle 1\over\displaystyle 3(m - 1)}\left( {... ...{\displaystyle 1\over\displaystyle 72}} \right) \approx 1,033. \end{displaymath}

Найдем теперь $В / С \approx \quad 12,75,\quad \mbox{а по приложению 5} \quad \chi_{кр}^2(0,01;5) = 15,1\quad\mbox{и}\quad \chi_{кр}^2 (0,05;5) = 11,1.$

Следовательно, $В \mathord{\left/ {\vphantom {В {С = 12,75 > 11,1 = }}} \right. \kern-\nulldelimiterspace} {С = 12,75 > 11,1 = }\chi_{кр}^2 (0,05;5)$ и нулевая гипотеза об однородности дисперсий по критерию Барлетта отклоняется на уровне значимости $\alpha $ = 0,05 и принимается на уровне значимости $\alpha = 0,01$, т.к. в этом случае $В \mathord{\left/ {\vphantom {В {С = 12,75 < 15,1 = }}} \right. \kern-\nulldelimiterspace} {С = 12,75 < 15,1 = }\chi _{кр}^2 (0,01;5).$

Пример 200. Анализ факторов, влияющих на обучение в информационно-обучающей среде, и степени их влияния на результаты обучения каждого участника эксперимента дали следующие результаты:

ранг Общего уровня усвоения знаний Интенсивности сам. работы По инструментальному типу

мотивации
№     начало экспер. конец экспер.
  1 4 2,5 1
  2 1 14 5,5
  3 6 7,5 3,5
  4 5 11 9,5
  5 7 2,5 3,5
  6 9 5 7
  7 2 13 14
  8 3 9 11
  9 12 4 2
  10 10 1 5,5
  11 8 6 9,5
  12 14 11 12,5
  13 11 7,5 8
  14 13 11 12,5

Найдите корреляционную матрицу анализа факторов, влияющих на обучение, для данного педагогического эксперимента.

Решение. Найдем все выборочные коэффициенты ранговой парной корреляции Спирмена данного эксперимента. Заметим, что третий и четвертый столбцы таблицы содержат одинаковые ранги, и поэтому в этих случаях, как и в рассмотренном примере 178 [перейти], рассчитаем и учтем поправки:


\begin{displaymath} T_3 = {\displaystyle 2 + 2\over\displaystyle 12} = {\display... ...over\displaystyle 12} = {\displaystyle 2\over\displaystyle 3}. \end{displaymath}

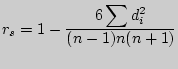$r_{12}$ вычислим по формуле Спирмена $r_s = 1 - {\displaystyle 6\sum {d_i ^2} \over\displaystyle (n - 1)n(n + 1)}$ при отсутствии одинаковых рангов:


\begin{displaymath} r_{12} = 1 - {\displaystyle 6(9 + 1 + 9 + 1 + 4 + 9 + 25 + 2... ...+ 4 + 1)\over\displaystyle 13 \cdot 14 \cdot 15} \approx 0,76. \end{displaymath}

Остальные коэффициенты парной корреляции вычисляем с учетом рассчитанных поправок по формуле 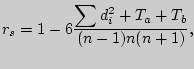$r_s = 1 - 6{\displaystyle \sum {d_i ^2} + T_a + T_b \over\displaystyle (n - 1)n(n + 1)},$ где в нашем случае $Т_{а}$ и $Т_{b}$ принимают два значения $1/3$ или $2/3$.


\begin{displaymath} r_{13} = 1 - 6{\displaystyle 427 + 1 \mathord{\left/ {\vphan... ...rspace} 3\over\displaystyle 13 \cdot 14 \cdot 15} \approx 0,6; \end{displaymath}


\begin{displaymath} r_{23} = 1 - 6{\displaystyle 577 + 1 \mathord{\left/ {\vphan... ...space} 3\over\displaystyle 13 \cdot 14 \cdot 15} \approx 0,13; \end{displaymath}


\begin{displaymath} r_{34} = 1 - 6{\displaystyle 74 + 1 \mathord{\left/ {\vphant... ...space} 3\over\displaystyle 13 \cdot 14 \cdot 15} \approx 0,84. \end{displaymath}

И тогда искомая корреляционная матрица выглядит следующим образом:


\begin{displaymath} {\rm {\bf (r)}} = \left[ {{\begin{array}{*{20}c} 1 \hfill &... ...hfill & \hfill & \hfill & 1 \hfill \\ \end{array} }} \right]. \end{displaymath}

Далее: Указатель обозначений Вверх: Глава V. Математическая статистика Назад: §39. Математическая статистика в

ЯГПУ, Центр информационных технологий обучения
2006-03-04