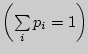 , а затем находим
основные характеристики
положения и рассеивания.
, а затем находим
основные характеристики
положения и рассеивания.
В этом параграфе рассматриваем по единому плану хорошо известные
распределения дискретных случайных величин. Во-первых, проверяем
выполняемость главного требования к закону распределения
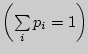 , а затем находим
основные характеристики
положения и рассеивания.
, а затем находим
основные характеристики
положения и рассеивания.
Пример 71. Равномерный закон распределения
Решение
1).
![]()
![]() Очевидно, что
Очевидно, что
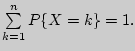
2). Характеристики положения
а). Математическое ожидание
б). Мода ![]() -
каждое значение с.в., поскольку все
-
каждое значение с.в., поскольку все
![]()
в). Медиана
![]() .
.
3). Для вычисления дисперсии воспользуемся формулой ![]() [
[![]() ] =
] = ![]() [
[
![]() [
[![]() ].
].
Найдем
![$M[X^2] = 1^2 \cdot {\displaystyle 1\over\displaystyle n} + 2^2 \cdot {\displays...
...+ 1)\over\displaystyle 6} = {\displaystyle (n + 1)(2n +
1)\over\displaystyle 6}$](img708.png) (см. [15], с. 73-74).
(см. [15], с. 73-74).
Тогда
![$D[X] = {\displaystyle (n + 1)(2n + 1)\over\displaystyle 6} - \left( {{\displays...
...style 12}[2(2n + 1) - 3(n + 1)] = {\displaystyle n^2 - 1\over\displaystyle 12}.$](img709.png)
Пример 72. Биномиальный закон распределения
Решение
1). С.в. ![]() = {число "успехов" при
= {число "успехов" при ![]() повторных независимых испытаниях}.
Тогда по формуле Бернулли
повторных независимых испытаниях}.
Тогда по формуле Бернулли
![]() (см. §
8). Используя бином Ньютона, получаем
(см. §
8). Используя бином Ньютона, получаем
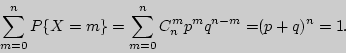
2). а). Для вычисления математического ожидания воспользуемся
индикатором
![]() (
(![]()
![]() "успехов" при
"успехов" при ![]() -м испытании (
-м испытании (![]() = 1, 2, ...,
= 1, 2, ..., ![]() . Тогда
. Тогда
поскольку ![]() (см. пример 61).
(см. пример 61).
б). ![]() -
наивероятнейшее число (см. §8).
-
наивероятнейшее число (см. §8).
3). Для нахождения дисперсии воспользуемся опять индикатором
"успехов" и
третьим свойством ![]() [
[![]() ]:
]:
поскольку ![]() (см. пример 64).
(см. пример 64).
Пример 73. Гипергеометрическое распределение. Из урны,
содержащей
![]() шаров, среди которых
шаров, среди которых ![]() белых, извлекаем
белых, извлекаем ![]() шаров. Составить закон
распределения для числа белых шаров, оказавшихся в выборке, и найти его
числовые характеристики.
шаров. Составить закон
распределения для числа белых шаров, оказавшихся в выборке, и найти его
числовые характеристики.
Решение. ![]() = {число белых шаров в выборке из
= {число белых шаров в выборке из ![]() шаров} = {0, 1,
2,...,
шаров} = {0, 1,
2,..., ![]() } и
} и
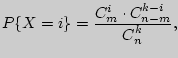 где
где ![]() = 0, 1, 2,...,
= 0, 1, 2,..., ![]() .
.
1).
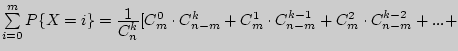
![]()
Использовали одно из свойств сочетаний (см. §3).
2). а). Математическое ожидание
![$ M[X] = \sum\limits_{i = 1}^m {i \cdot {\displaystyle C_m^i \cdot C_{n - m}^{k ...
...\cdot C_{n - m}^{k - 1} +
2 \cdot C_m^2 \cdot C_{n - m}^{k - 2} + ...+}\right. $](img722.png)
![$\left. { + m \cdot C_m^m \cdot C_{n -
m}^{k - m} } \right]
= {\displaystyle k!...
...ystyle m(m -
1)\over\displaystyle 2} \cdot 2 \cdot C_{n - m}^{k - 2} + }\right.$](img723.png)
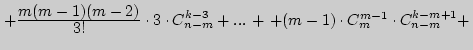
![]()
![]()
![]()
б). Моду ![]() находим аналогично определению
наивероятнейшего числа биномиального закона распределения из решения
системы
неравенств:
находим аналогично определению
наивероятнейшего числа биномиального закона распределения из решения
системы
неравенств:
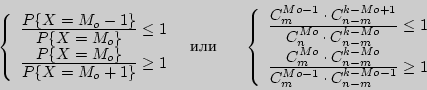
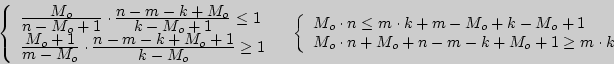
Откуда получаем
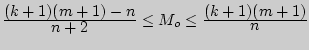 и
и ![]()
3). Прямое вычисление дисперсии громоздко, поэтому ![]() [
[![]() ] найдем позднее с
использованием ковариации (см. пример 110).
] найдем позднее с
использованием ковариации (см. пример 110).
В последних трех примерах рассмотрены конечные случайные величины.
Пример 74. Распределение Пуассона
Решение. Распределение Пуассона можно получить из биномиального,
приняв за
![]() = np и устремив число испытаний
= np и устремив число испытаний ![]() в бесконечность. В самом деле
в бесконечность. В самом деле
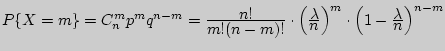 по
формуле Бернулли и при
по
формуле Бернулли и при
![]()
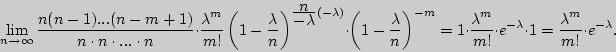
1). Рассмотрим бесконечное дискретное распределение
![]() ,
где 0 <
,
где 0 < ![]() - параметp, a
- параметp, a ![]() =
0, 1, 2, ...Проверим, что
=
0, 1, 2, ...Проверим, что
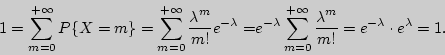
2). а). Математическое ожидание
![\begin{displaymath}
M[X] = \sum\limits_{m = 0}^\infty {m \cdot {\displaystyle \l...
... = e^{ - \lambda } \cdot \lambda \cdot
e^\lambda = \lambda } .
\end{displaymath}](img738.png)
б). ![]() =
0, если 0 <
=
0, если 0 < ![]() <1.
<1.
3). Дисперсия
![\begin{displaymath}
\begin{array}{l}
M[X^2] = \sum\limits_{m = 0}^\infty {m^2{\...
...a e^\lambda } \right] =
\lambda ^2 + \lambda . \\
\end{array}\end{displaymath}](img739.png)
Следовательно,
![]()
Пример 75. Геометрическое распределение
Решение.
1). Проводим повторные независимые испытания до появления "успеха". Граф распределения в этом случае выглядит следующим образом.
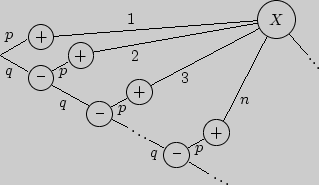
![]() где
где
![]()
Проверим, что
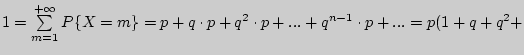
![]()
2). а). Математическое ожидание
![]()
![]()
б). ![]() =
1, т.к.
=
1, т.к. ![]() = max {
= max {![]() {
{![]() },
}, ![]() = 1, 2,
3, ...}.
= 1, 2,
3, ...}.
в). Для нахождения ![]() решим систему неравенств
решим систему неравенств
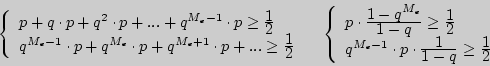
Отсюда
![]()
3). Для вычисления дисперсии найдем
![\begin{displaymath}
\begin{array}{l}
M[X^2] = \sum\limits_{k = 1}^\infty {k^2q^...
...= {\displaystyle 1 + q\over\displaystyle p^2}. \\
\end{array}\end{displaymath}](img752.png)
Тогда
![]()
Вопросы для самоконтроля
Задачи