Далее: §15. Классические распределения Вверх: Глава III. Случайные величины Назад: §13. Закон и функция

§14. Числовые характеристики дискретных случайных величин

Пусть дана случайная величина $X(\omega ) \quad \nu $а $\Omega $. Если ряд $\sum\limits_{\omega \in \Omega } {X(\omega )P(\omega )} $ сходится абсолютно, то его сумма $\sum\limits_{\omega :\omega \in \Omega } {X(\omega ) \cdot P(\omega )} = M[X]$ называется математическим ожиданием (м.о.) с.в. $X$.

Свойства математического ожидания:

  1. $M$[$C$] = $C$, где $C$ - const;
  2. $M$[$C\cdot X$] = $C\cdot M$[$X$];
  3. $M$[X $\pm $ Y] = $M$[$X$] $\pm M$[$Y$];
  4. $M$[X$\cdot $Y] = $M$[$X$] $\cdot M$[$Y$], где $X$ и $Y$ - независимые с.в.

Случайные величины $X$ и $Y$ называются независимыми, если для любых $x_{i}$, $y_{j}$ имеет место равенство $P\{X = x_i ,Y = y_j \} = P\{X = x_i \}P\{Y = y_j \}$.

Модой $M_{{\text{ о}}}$ д.с.в. называется ее наиболее вероятное значение.

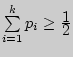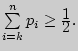Медианой $M_{{\text{ е}}}$ ряда значений $x_{1}$ < $x_{2}$ <...< $x_{n}$, которые с.в. $X$ принимает с вероятностями $p_{1}$, $p_{2}$, ..., $p_{n}$ соответственно, называется значение $x_{k}$ с таким индексом $k$, что $\sum\limits_{i = 1}^k {p_i \ge {\displaystyle 1\over\displaystyle 2}} $ и $\sum\limits_{i = k}^n {p_i \ge {\displaystyle 1\over\displaystyle 2}} .$ Это означает, что приблизительно одинаково вероятно, продолжится ли процесс после медианы или закончится до нее.

Если математическое ожидание с.в. $X^s$ существует, то оно называется начальным моментом $\alpha _{s}$[$X$] порядка $s$ с.в. $X$:


\begin{displaymath} \alpha _s [X] = M[X^s] = \sum\limits_i {x_i ^sp_i .} \end{displaymath}

Поскольку $\left\vert X \right\vert^{s - 1} \le \left\vert X \right\vert^s + 1,$ то из существования $\alpha _{s}$[$X$] вытекает существование $\alpha _{s - 1}$[$X$] и, следовательно, существование всех начальных моментов порядка меньше $s-1.$

Математическое ожидание с.в. является ее первым начальным моментом:


\begin{displaymath} M[X] = \alpha _1 [X]. \end{displaymath}

Начальные моменты, мода и медиана являются характеристиками положения случайной величины.

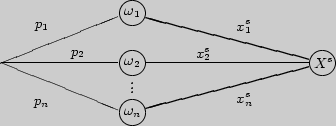
Начальный момент $\alpha _{s}$[$X$] д.с.в. можно находить как вес всего графа распределения с.в. $X^s$:


\includegraphics{D:/html/work/link1/metod/met12/23_ris47.eps}

Рис. 47


\begin{displaymath} \alpha _s [X] = \sum\limits_i {x_i ^sp_i } \end{displaymath}

Понятие математического ожидания случайной величины ввели в середине XVIIв. Гюйгенс и Схоутен.

Пример 66. Найти начальные моменты индикатора события $A$.

Решение. $\alpha _s [I_A ] = M[I_A ^s] = 0^3 \cdot q + 1^3 \cdot p = p.$

Пример 67. (Санкт-Петербургский парадокс: см. [52], с. 35-38.).

Бросаем монету до тех пор, пока не выпадет решка; если это произойдет при $r$-м бросании, игрок получает из банка 2$^{r}$ долларов. Сколько следует заплатить игроку за участие в игре, чтобы игра стала безобидной?

Решение. Безобидность игры рассматриваем в классическом смысле: математическое ожидание чистого выигрыша должно быть равно 0.

Пусть $X$ = {величина выигрыша игрока}. Составим граф распределения для $X$:


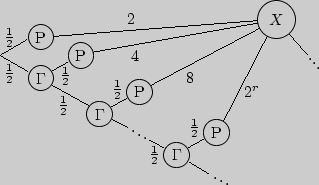
\includegraphics{D:/html/work/link1/metod/met12/24_ris48.eps}

Рис. 48


\begin{displaymath} M[X] = {\displaystyle 1\over\displaystyle 2} \cdot 2 + {\dis... ...laystyle 2}} \right)^r \cdot 2^r + ... = 1 + 1 + ... + 1 + ... \end{displaymath}

Следовательно, выигрыш игрока имеет бесконечное математическое ожидание, и игра стала бы безобидной при бесконечном взносе, что невозможно.

Решим эту задачу при естественном предположении об ограниченности ресурсов банка. Пусть в данный момент в банке имеется 100 тыс. долларов (2$^{17}$ = 131072 > 10$^{5})$, и условимся, что если решка впервые выпадет при 17-м бросании монеты или еще позднее, то банк отдает все имеющиеся у него в настоящее время доллары, т.е. 100 тыс. долларов. Тогда


\begin{displaymath} \begin{array}{l} M[X] = {\displaystyle 1\over\displaystyle ... ...yle 4} + ...} \right) \approx 16 + 1,5 = 17,5. \\ \end{array}\end{displaymath}

Следовательно, при вступительном взносе игрока, равном 17,5 долларов, игра будет безобидной, а при большем взносе станет выгодной для банка.

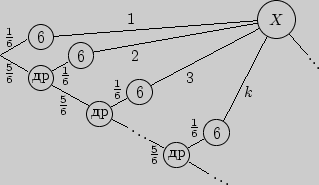
Пример 68. Бросаем игральную кость до появления шестерки. Если это произойдет при $k$-м бросании, то игрок получит приз в $k$ рублей. Какой вступительный взнос следует заплатить игроку, чтобы игра стала безобидной?

Решение. Пусть $X$ = {величина приза}, тогда с.в. имеет следующий граф распределения:


\includegraphics{D:/html/work/link1/metod/met12/25_ris49.eps}

Рис. 49


\begin{displaymath} \begin{array}{l} M[X] = {\displaystyle 1\over\displaystyle ... ...ystyle 5\over\displaystyle 6}} \right)^2} = 6. \\ \end{array}\end{displaymath}

Итак, для того, чтобы игра была безобидной, вступительный взнос должен составлять 6 рублей.

Это пример геометрического распределения, для которого

$P\{X = k\} = q^{k - 1} \cdot p,$ где $k$ = 1, 2, ...

Центрированной с.в. называется отклонение с.в. от ее математического ожидания:


\begin{displaymath} \mathop X\limits^o = X - M[X] = X - \bar {x}. \end{displaymath}

Центральным моментом порядка $s$ с.в. $X$ называется м.о. $s$-й степени центрированной с.в.:


\begin{displaymath} \mu _s [X] = M[\mathop X\limits^o ] = M[(X - \bar {x})^s]. \end{displaymath}

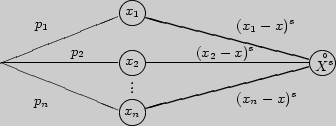
Для вычисления центральных моментов удобно использовать следующий граф:


\includegraphics{D:/html/work/link1/metod/met12/26_ris50.eps}

Рис. 50


\begin{displaymath} \mu _s [X] = \sum\limits_i {p_i (x_i - \bar {x})^s} . \end{displaymath}

Центральные моменты характеризуют рассеивание с.в. и выражаются через начальные моменты по следующим формулам:


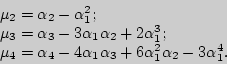
\begin{displaymath} \begin{array}{l} \mu _2 = \alpha _2 - \alpha _1 ^2; \\ \m... ...a _3 + 6\alpha _1 ^2\alpha _2 - 3\alpha _1 ^4. \\ \end{array}\end{displaymath}

Особое значение для практики имеет второй центральный момент $\mu $$_{2}$, который называется дисперсией с.в. $X$:


\begin{displaymath} D[X] = \mu _2 = M[(X - \bar {x})^2] = \sum\limits_i {(x_i - \bar {x})} ^2p_i. \end{displaymath}

Для вычисления $D$[$X$] удобна следующая формула:

$D[X] =M[X^{2}]-M^{2}[X].$

Свойства дисперсии:

  1. $D$[$C$] = 0, где $C$ - const;
  2. $D$[$C\cdot X$] = $C\cdot D$[$X$];
  3. $D$[X $\pm $ Y] = $D$[$X$] + $D$[$Y$], если $X$, $Y$ - независимые с.в.

Дисперсия имеет размерность квадрата с.в. Положительное значение квадратного корня из дисперсии называется средним квадратичным отклонением (или стандартным отклонением):


\begin{displaymath} \sigma [X] = \sigma _X = + \sqrt {D[X]} . \end{displaymath}

Впервые термины "стандартное отклонение" и "дисперсия" использовались К. Пирсоном в 1895 г. и Р. Фишером в 1920 г.

Пример 69. Найти центральные моменты индикатора события $A$.

Решение. $\mu _s = M[(I_A - p)^s] = ( - p)^sq + q^sp = pq[( - 1)^sp^{s - 1} + q^{s - 1}].$

Пример 70. Случайная величина $X^\ast = (X - \bar {x}) / \sigma_x .$ Доказать, что $M[X^\ast ] = 0$ и $D[X^\ast ] = 1, \quad (\alpha x + \beta )^\ast = X^\ast $, если $\alpha > 0 $ и если $\alpha < 0$, то $(\alpha x + \beta )^\ast = - X^\ast .$

Решение. Используя свойства математического ожидания и дисперсии, получаем


\begin{displaymath} M[X^\ast ] = M[(X - \bar {x}) / \sigma _x ] = {\displaystyle... ...style 1\over\displaystyle \sigma _x }(M[X] - M[\bar {x}]) = 0, \end{displaymath}


\begin{displaymath} D[X^\ast ] = D[(X - \bar {x}) / \sigma _x ] = \left( {{\disp... ...displaystyle \sigma _x ^2\over\displaystyle \sigma _x ^2} = 1, \end{displaymath}


\begin{displaymath} (\alpha x + \beta )^\ast = [(\alpha x + \beta ) - (\alpha \b... ...ver\displaystyle \left\vert \alpha \right\vert} \cdot X^\ast . \end{displaymath}

Вопросы для самоконтроля

  1. Какие характеристики положения вы знаете?
  2. Вероятностный смысл моды и медианы.
  3. Сколько у случайной величины мод и медиан?
  4. Свойства математического ожидания.
  5. Всегда ли существует математическое ожидание случайной величины?
  6. Что характеризуют центральные моменты?
  7. Назовите основные характеристики рассеивания.
  8. Нахождения числовых характеристик дискретных случайных величин по графу распределения.

Задачи

I 131. Из урны, содержащей три шара с номерами 1, 2 и 3, последовательно достают два шара. Найти математические ожидания сумм номеров извлеченных шаров, если шары достают с возвратом и без возврата.

  132. Найти математические ожидания сумм выпавших очков при подбра-сывании костей, если:
а) бросают один раз одну кость;
б) бросают один раз две кости;
в) бросают вместе две кости сто раз.

  133. Случайная величина $X$ принимает три значения: $x_{1}$= 1, $x_{2}$= 2, $x_{3}$ = 3. Известны математическое ожидание и дисперсия этой величины: $M$[$X$] = 2,3 и $D$[$X$] = 0,61. Найти закон распределения для случайной величины $X$.

  134. Биатлонист поражает мишень из положения лежа с вероятностью 0,9, а из положения стоя с вероятностью - 0,7. Найти математическое ожида-ние суммарного числа пораженных мишеней при десяти выстрелах из каждого положения.

  135. Найти дисперсию для числа выпавших "гербов" при подбрасывании одной монеты; двух и ста монет.

  136. Найти средние квадратичные отклонения для сумм выпавших очков при двух и десяти подбрасываниях игральной кости.

II 137. Случайные величины $X$ и $Y$ заданы законами распределения:

$X$ 1 3
$P$ 0,2 0,8
                
$Y$ 0 2 4
$P$ 0,5 0,4 0,1

Найти характеристики положения и рассеивания случайной величины $X+Y$.

  138. Какую игру вы выбираете: с призом 8 руб. за выпадение по крайней мере одного "герба" или с призом в 16 руб. за выпадение двух "гербов" при трех подбрасываниях монеты?

III 139. Найти начальные и центральные моменты до пятого порядка для индикатора события $A$.

  140. Доказать разумность или опровергнуть идею мартингальной системы, заключающейся в удвоении ставки при проигрыше. (Предположим, что мы играем в рулетку и всегда ставим на красное. Сначала поставим один доллар. Если выигрываем, то прекращаем игру; при проигрыше ставим в следующий раз 2 доллара и т.д.).
Далее: §15. Классические распределения Вверх: Глава III. Случайные величины Назад: §13. Закон и функция

ЯГПУ, Центр информационных технологий обучения
2006-03-04