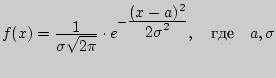 - параметры.
- параметры.
В начале XIX века нормальное распределение затмило собой все остальные, поскольку в работах Гаусса и Лежандра утверждалось о нормальном законе распределения ошибок наблюдений.
Нормальный закон распределения (или распределение Гаусса) задается следующей дифференциальной функцией
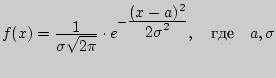 - параметры.
- параметры.
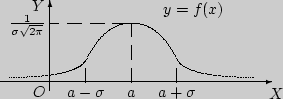
![]() (
(![]() - max
- max
![]() = а -
= а - ![]() , x
, x![]() = а +
= а + ![]() - точки перегиба.
- точки перегиба.
Пример 91. Показать, что функция
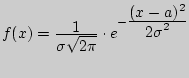 является
дифференциальной функцией распределения н.с.в.
является
дифференциальной функцией распределения н.с.в.
Решение. Проверим, что
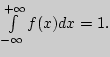
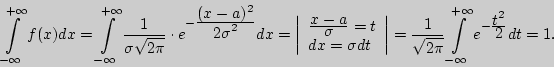
Пример 92. Правило трех сигм.
Решение. Найдем вероятность того, что распределенная нормально
с.в. ![]() находится на промежутке ]
находится на промежутке ] ![]() ,
, ![]() [ .
[ .
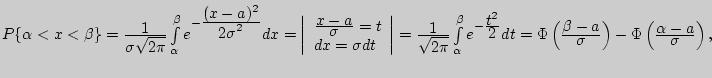 - табличная функция Лапласа (см. §9[перейти] и приложение 2).
- табличная функция Лапласа (см. §9[перейти] и приложение 2).
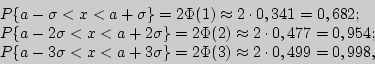
т.е. можно считать практически достоверным, что случайная величина,
распределенная по нормальному закону, находится на интервале ]
![]() [.
[.
Пример 93. Найти характеристики положения для нормального закона распределения.
Решение. 1).
![$M[X] = {\displaystyle 1\over\displaystyle \sigma \sqrt {2\pi } }\int\limits_{ -...
... +
\infty } {e^{ - {\displaystyle t^2\over\displaystyle 2}}(\sigma t + a)dt} = $](img902.png)
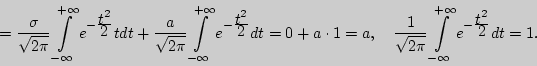
2).
 то
то ![]() .
.
3). ![]() , т.к. график функции
, т.к. график функции
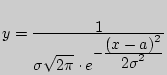 симметричен относительно прямой
симметричен относительно прямой ![]() .
.
Пример 94. Найти характеристики рассеивания для нормального закона распределения.
Решение. 1).
![$D[X] = {\displaystyle 1\over\displaystyle \sigma \sqrt {2\pi } }\int\limits_{ -...
... \infty }^{ + \infty }
{t^2e^{ - {\displaystyle t^2\over\displaystyle 2}}dt} = $](img909.png)
![\begin{displaymath}
\left\vert {\begin{array}{l}
u = t \\
dv = te^{ - {\displ...
...splaystyle t^2\over\displaystyle 2}}dt} } \right] =
\sigma ^2.
\end{displaymath}](img910.png)
2). Среднее квадратическое отклонение
![]() в нашем
случае равно
в нашем
случае равно ![]() .
.
3). Найдем асимметрию ![]() .
.
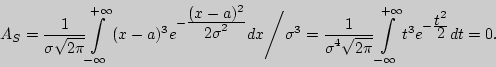
Пример 95. Найти математическое ожидание и дисперсию для показательного двустороннего закона Лапласа.
Решение. 1).
![$M[X] = \int\limits_{ - \infty }^{ + \infty } {x{\displaystyle \lambda
\over\dis...
...
\over\displaystyle 2}\int\limits_a^{ + \infty } {xe^{ - \lambda (x - a)}dx} = $](img914.png)

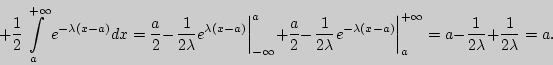
2). Для нахождения дисперсии вычислим M[X![]() ]:
]:
![\begin{displaymath}
M[X^2] = \int\limits_{ - \infty }^{ + \infty } {x^2{\display...
...e 2}\int\limits_a^{ +
\infty } {x^2e^{ - \lambda (x - a)}dx} =
\end{displaymath}](img917.png)
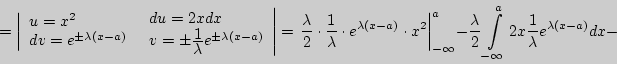

Вопросы для самоконтроля
Как задается нормальный закон распределения?
Свойства дифференциальной функции распределения нормального закона.
Как изменяется кривая нормального распределения при изменении ее параметров?
Какие числовые характеристики нормального распределения совпадают?
Как можно находить математическое ожидание и среднее квадратичное отклонение по кривой нормального распределения?
Каким образом можно получить асимптотическую формулу Лапласа?
Правило трех сигм.
Задачи
I 181. Математическое ожидание нормально распределенной
случайной величины ![]() равно
равно ![]() и среднее квадратическое
отклонение
и среднее квадратическое
отклонение ![]() = 3. Написать дифференциальную
функцию распределения для
= 3. Написать дифференциальную
функцию распределения для ![]() .
.
182. Найти плотность вероятности нормально распределенной
случайной величины ![]() , зная, что
, зная, что ![]() [
[![]() ] = 2,
] = 2, ![]() [
[![]() ] = 9.
] = 9.
183. Случайная величина ![]() задана дифференциальной функцией
задана дифференциальной функцией
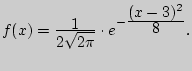 Найти математическое ожидание и дисперсию
Найти математическое ожидание и дисперсию ![]() .
.
184. Нормально распределенная случайная величина ![]() задана
функцией плотности вероятности
задана
функцией плотности вероятности
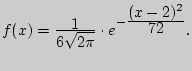 Найти моду и медиану
Найти моду и медиану ![]() .
.
185. Случайная величина ![]() распределена по нормальному закону с
распределена по нормальному закону с
![]() и
и ![]() = 0,5. Определить вероятность того,
что ее значение отклоняется от
= 0,5. Определить вероятность того,
что ее значение отклоняется от ![]() по
абсолютной величине не более чем на 0,7.
по
абсолютной величине не более чем на 0,7.
186. Случайная величина ![]() задана дифференциальной функцией
задана дифференциальной функцией
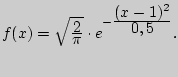 Найти вероятность того, что случайная величина попадет в интервал
(0, 2).
Найти вероятность того, что случайная величина попадет в интервал
(0, 2).
II 187. Случайная величина ![]() распределена нормально со
средним квадратическим отклонением
распределена нормально со
средним квадратическим отклонением ![]() = 2 мм.
Найти длину интервала, симметричного относительно математического
ожидания, в который с вероятностью 0,995 случайная величина
= 2 мм.
Найти длину интервала, симметричного относительно математического
ожидания, в который с вероятностью 0,995 случайная величина ![]() оба раза попадет в результате двух испытаний.
оба раза попадет в результате двух испытаний.
188. Случайная величина ![]() распределена нормально и имеет
плотность вероятности
распределена нормально и имеет
плотность вероятности
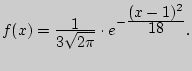 Найти математическое ожидание и
дисперсию случайной величины
Найти математическое ожидание и
дисперсию случайной величины ![]() , если
, если ![]() = 5
= 5![]() +1.
+1.
III 189. Случайная величина ![]() распределена по
нормальному закону с плотностью вероятности
распределена по
нормальному закону с плотностью вероятности
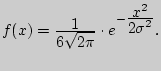 Найти дифференциальную функцию обратной ей величины
Найти дифференциальную функцию обратной ей величины ![]() = 1/
= 1/![]() .
.
190. Доказать, что если случайная величина ![]() имеет нормальное
распределение, то линейная функция
имеет нормальное
распределение, то линейная функция
![]() также имеет нормальное распределение.
также имеет нормальное распределение.