Далее: Об этом документе ... Вверх: Термодинамика Назад: 8.  Замечательные задачи

9.  Ответы и решения

Вопросы и задачи к разделу 2
"Работа и теплота"

2.1. Поглощенное телом тепло определяется как произведение его массы на удельную теплоемкость и разность конечной и начальной температур:

$$Q\ =\ m\,c\,\Delta t\;.$$

В случае, когда результат получается отрицательным, говорят, что тело выделяет тепло.

Равновесие в теплоизолированной системе, состоящей из нескольких тел, устанавливается в соответствии с уравнением теплового баланса, которое выражает равенство количеств поглощенного и выделенного разными телами тепла:

$$Q_{1}\ +\ Q_{2}\ +\ .\ .\ .\ =\ 0\;.$$

Для нашей системы уравнение теплового баланса имеет следующий вид⁷:

$$m_{1}\,c_{1}\,(t-t_{1})\ +\ m_{2}\,c_{2}\,(t-t_{1}) \ +\ m_{3}\,c_{3}\,(t-t_{3})\ =\ 0\;.$$

Отсюда удельная теплоемкость стали равна

$$c_{3}\ =\ \frac{(m_{1}\,c_{1}\,+\,m_{2}\,c_{2})\,(t-t_{1})} {... ...\,(t_{3}-t)}\ \approx\ 0,112\ \text{ккал/кг}\cdot\text{град}\;.$$

2.2. Охлаждение воздуха внутри шарика происходит при постоянном атмосферном давлении. Так как воздух при атмосферном давлении близок по свойствам к идеальному газу, к нему можно применить закон Гей-Люссака:

$$\frac{V}{T}\ =\ \frac{V_{0}}{T_{0}}\;\;\;\;\mbox{или} \;\;\;\;\;\;V\ =\ V_{0}\,\frac{T}{T_{0}}\;.$$

Здесь $V_{0}$ и $T_{0}$ - объем и температура воздуха внутри шарика в начальном состоянии, $V$ и $T$ - его объем и температура после охлаждения.

Работа, совершенная над шариком при постоянном давлении, определяется как

$$A_{\text{вн}}\ =\ p_{0}\,(V_{0}\,-\,V)\ = \ p_{0}\,V_{0}\,\frac{T_{0}-T}{T_{0}} \ \approx\ 121\ \text{ Дж}\;.$$

Тепло, выделенное при охлаждении воздуха в шарике при постоянном значении давления, равно

$$Q\ =\ c_{p}\,m\,(T_{0}\,-\,T)\ = \ c_{p}\,\rho\,V_{0}\,(T_{0}\,-\,T)\ \approx\ 420\ \text{ Дж}\;.$$

Отношение внешней работы к выделенному теплу

$$\frac{A_{\text{вн}}}{Q}\ =\ \frac{p_{0}}{T_{0}\,c_{p}\,\rho}\ \approx \ 0,29$$

не зависит от конечных значений температуры, объема и плотности воздуха.

Обратим внимание, что работа и тепло здесь измеряются в одинаковых единицах - джоулях. Причина этого выясняется в разделе 3.

Вопросы и задачи к разделу 3
"Первое начало термодинамики"

3.1. В изобарном процессе часть поглощенного тепла расходуется на совершение полезной работы, поэтому для увеличения температуры на фиксированную величину требуется больше тепла, чем в изохорном процессе, то есть теплоемкость $C_{v}$ всегда меньше теплоемкости $C_{p}$.

3.2. Ответ на этот вопрос дан в разделе 8 на странице [перейти]. Если температура газа изменяется в изохорном процессе, то работа не совершается, и все поглощенное (выделенное) тепло идет на увеличение (уменьшение) внутренней энергии:

$$\Delta U\ =\ \Delta Q\ =\ \frac{m}{\mu}\,C_{v}\,\Delta T\;,$$

где $m$ и $\mu$ - соответственно масса и молярная масса газа.

Далее заметим, что систему всегда можно перевести из произвольного состояния 1 с температурой $T_{1}$ в другое произвольное состояние 2 с температурой $T_{2}$ путем последовательного совершения изохорного и изотермического процесса (в любой последовательности), а изотермические процессы не изменяют значения внутренней энергии идеального газа. В феноменологической термодинамике это свойство является определением идеального газа, то есть идеальным, собственно, и называется газ, обладающий данным свойством.

С молекулярной точки зрения изотермическое изменение объема и давления идеального газа также не изменяет его внутреннюю энергию. Это ясно из следующих соображений. Во внутренюю энергию идеального газа дают вклад лишь кинетические энергии молекул, а они зависят только от температуры и не зависят от объема и давления⁸. Иными словами, поскольку взаимодействие на расстоянии между молекулами отсутствует, любой молекуле "безразлично", на каком расстоянии от нее находятся остальные молекулы, то есть какой объем занимает газ, в то же время ей "небезразлично", какими кинетическими энергиями обладают другие молекулы, то есть какова температура газа, так как кинетические энергии отдельных молекул в результате множества столкновений в среднем равны друг другу.

Таким образом, внутренняя энергия идеального газа является однозначной функцией температуры; ее изменение при изменении температуры от $T_{1}$ до $T_{2}$ равно

$$\Delta U\ =\ \frac{m}{\mu}\,C_{v}\,(T_{2}\,-\,T_{1})\;,$$

независимо от значений давления и объема в начальном и конечном состояниях. В частном случае, для изобарных и изохорных процессов, данный результат уже получен нами при решении задачи на с. [перейти].

3.3. В обоих случаях в начальном состоянии объем газа - $V_{1}$, давление - $p_{1}$, следовательно, определена и температура газа - $T_{1}$. Изотермическое расширение сопровождается поглощением тепла в количестве, необходимом для поддержания постоянной температуры. В процессе адиабатического расширения работа совершается только за счет уменьшения внутренней энергии, следовательно, газ при этом охлаждается.

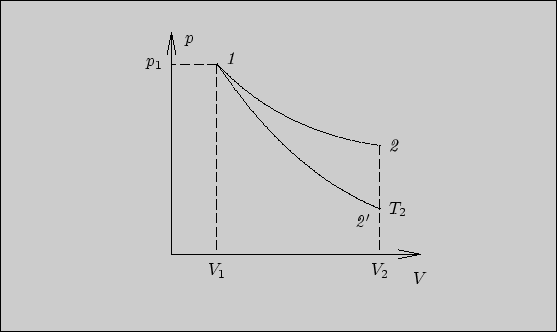
Рис. 23 

Таким образом, в конечном состоянии приизотермическом расширении температура остается
прежней - $T_{1}$, а в случае адиабатического расширения становится меньше: $T_{2}<T_{1}$.

При одном и том же конечном объеме $V_{2}$ более низкой температуре газа будет соответствовать и меньшее значение давления, то есть конечное давление будет больше при изотермическом расширении. Другими словами, в точке пересечения изотермы и адиабаты на диаграмме $(p,V)$ изотерма изображается более пологой кривой (рис. 23).

3.4. Может, если совершаемая над газом внешняя работа больше, чем прирост внутренней энергии:

$$Q\ =\ \Delta U\ -\ A_{\text{вн}}\ <\ 0\;.$$

В этом случае теплоемкость газа отрицательна.

Процессам с отрицательной теплоемкостью на диаграмме $(p,V)$ соответствуют кривые, наклон которых имеет промежуточное значение между наклоном изотермы и адиабаты (см. рис. 23). Действительно, для изотермы $Q\,=\,-A_{\text{вн}}$ и $\Delta U=0\;\;$⁹, а для адиабаты $Q=0$ и $\Delta U\,=\,A_{\text{вн}}$. Следовательно, в промежуточном случае для сжатия $-A_{\text{вн}}<Q<0$ и $0<\Delta U<A_{\text{вн}}$ (в случае расширения неравенства изменяются на противоположные и при охлаждении газа происходит поглощение тепла).

3.5. Как уже отмечалось, при адиабатическом расширении газ совершает работу за счет уменьшения внутренней энергии:

$$\Delta U_{1}\ =\ -\,A\;.$$

В изохорном процессе работа не совершается, то есть все поглощенное тепло идет на увеличение внутренней энергии:

$$\Delta U_{2}\ =\ Q\;.$$

По условию $A\,=\,Q$, следовательно, суммарное изменение внутренней энергии за два процесса

$$\Delta U\,=\,0\;.$$

Для идеального газа между температурой и внутренней энергией существует взаимно однозначное соответствие, выражаемое формулой (16):

$$U\ =\ \frac{m}{\mu}\,C_{v}\,T\;.$$

Следовательно, конечная температура будет совпадать с начальной. Графическое изображение процессов на диаграмме $(p,V)$ соответствует участкам ${\it 1 \rightarrow 2^{\prime}}$ и ${\it 2^{\prime} \rightarrow 2}$ на рис. 23. При этом конечное состояние изохорного участка в условиях поставленного вопроса точно попадает на изотерму ${\it 1 \rightarrow 2}$ только для идеального газа.

3.6. Описанный опыт является одним из вариантов известного опыта Джоуля по регистрации изменения температуры при расширении газов в пустоту в теплоизолирующей оболочке. В условиях поставленного вопроса теплоизоляция обеспечивается тем, что полость находится внутри сосуда с газом, то есть не имеет непосредственного теплового контакта с внешними телами, а также быстротой протекания процесса.

С точки зрения первого начала термодинамики при адиабатическом расширении идеального газа в пустоту сохраняется его внутренняя энергия и, следовательно, температура, так как отсутствует теплообмен с внешней средой и не совершается работа (из-за отсутствия внешних сил). Для реальных газов в описанном процессе внутренняя энергия и температура незначительно изменяются, так как увеличивается среднее расстояние между молекулами и при этом силами межмолекулярного взаимодействия совершается работа.

В опыте Джоуля проявлялись небольшие изменения температуры, причем для одних газов температура увеличивалась, а для других - уменьшалась. Чрезвычайно малая величина изменений температуры позволила Джоулю впервые ввести понятие идеального газа - такого газа, для которого при адиабатическом расширении в пустоту температура не изменяется (изменение пренебрежимо мало). Известное определение идеального газа с позиций молекулярной структуры было дано позднее.

3.7. Рассмотрим изобарное расширение одного моля идеального газа из состояния 1 в состояние 2. В данном процессе поглощается количество тепла

$$Q_{12}\ =\ C_{p}\,(T_{2}\,-\,T_{1})\;,$$

происходит увеличение внутренней энергии

$$\Delta U_{12}\ =\ C_{v}\,(T_{2}\,-\,T_{1})$$

и совершается работа

$$A_{12}\ =\ p\,(V_{2}\,-\,V_{1})\;.$$

Используя уравнение состояния идеального газа, выразим работу через конечную и начальную температуры:

$$A_{12}\ =\ R\,(T_{2}\,-\,T_{1})\;.$$

Тогда, в соответствии с первым началом термодинамики, окончательно получим

$$C_{p}\,(T_{2}\,-\,T_{1})\ =\ C_{v}\,(T_{2}\,-\,T_{1})\ +\ R\,(T_{2}\,-\,T_{1})\;,$$

или

$$C_{p}\,-\,C_{v}\ =\ R\;.$$

3.8. Из уравнения состояния идеального газа

$$p\,V\ =\ \frac{m}{\mu}\,R\,T$$

выразим универсальную газовую постоянную:

$$R\ =\ \frac{p\,\mu}{\rho\,T}\;.$$

За исключением молярной массы воздуха, у нас имеются все данные для вычисления этой величины, причем они заданы в единицах СИ, так что $R$ будет выражена в единицах Дж/град.

Из соотношения Майера для удельных теплоемкостей получаем

$$c_{p}\,-\,c_{v}\ =\ \frac{R^{\prime}}{\mu}\;\;\;.$$

Отсюда для газовой постоянной $R^{\prime}$ имеем

$$R^{\prime}\ =\ \mu\,c_{p}\,\left(\frac{\gamma\,-\,1}{\gamma}\right)\;\;\;,$$

причем имеющиеся данные (кроме $\mu$) позволяют выразить ее в ккал/град. Тогда механический эквивалент тепла $J$ можно выразить как отношение:

$$J\ =\ \frac{R}{R^{\prime}}\cdot10^{-3}\ = \ \frac{\gamma\,p\cdot10^{-3}}{c_{p}\,(\gamma\,-\,1)\,\rho\,T}\;.$$

Предполагается, что все величины в этой формуле используются в тех единицах, в которых они заданы в задаче, а температура переводится в абсолютную шкалу: $T\, =\, 273\ K$. Подстановка численных значений дает

$$J\ =\ \frac{1,405\cdot 1,013\cdot 10^{5}\cdot 10^{-3}} {0,238\cdot 0,405\cdot 1,29\cdot 273}\ \approx\ 4,19\ \text{ Дж/кал}\;.$$

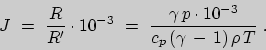
3.9. Согласно первому началу термодинамики, изменение внутренней энергии представляет собой разность между поглощенным теплом и совершенной работой. Поглощенное тепло в нашем случае выражается как

$$Q\ =\ q\,m\;,$$

где $q$ - удельная теплота парообразования, $m$ - масса испарившейся жидкости. Работа определяется как произведение атмосферного давления на разность объемов пара и жидкости. Так как по условию объемом жидкости можно пренебречь, то

$$A\ =\ p_{0}\,m\,v\;,$$

где $p_{0}$ - атмосферное давление, $v$ - удельный объем пара. Таким образом, для изменения внутренней энергии получаем:

$$\Delta U\ =\ m\,(q\,-\,p_{0}\,v)\ \approx\ 15,9\ \text{ кДж}\;.$$

Величина атмосферного давления берется при нормальных условиях (см. данные предыдущей задачи).

3.10. По условию температуры в состояниях 1 и 2 равны, что для идеального газа означает равенство внутренних энергий. Отсюда следует, что поглощенное в процессе ${\it 1 \rightarrow 2}$ тепло равно совершенной работе:

$$Q_{12}\ =\ A_{12}\ =\ \frac{1}{2}\,(p_{1}\,+\,p_{2})\,(V_{2}\,-\,V_{1})\;.$$

Количество тепла, выделенное в изобарном процессе ${\it 2\rightarrow3}$, составляет

$$\mid Q_{23}\mid \ =\ \nu\,C_{p}\,(T_{2}\,-\,T_{3})$$

($\nu$ - количество молей газа). Пользуясь уравнением состояния идеального газа, выразим $\mid Q_{23}\mid$ через давление $p_{2}$ и объемы $V_{2}$ и $V_{1}$:

$$\mid Q_{23}\mid \ =\ \frac{C_{p}}{R}\ p_{2}\,(V_{2}\,-\,V_{1})\;.$$

Отношение поглощенного тепла к выделенному, таким образом, равно

$$\frac{Q_{12}}{\mid Q_{23}\mid} \ =\ \frac{(p_{1}/p_{2}\,+\,1)\,R}{2\,C_{p}}\;\;.$$

Из равенства температур в состояниях 1 и 2 для идеального газа следует, что

$$p_{1}\,V_{1}\ =\ p_{2}\,V_{2}\;,$$

или

$$\frac{p_{1}}{p_{2}}\ =\ \frac{V_{2}}{V_{1}}\ =\ 2,5\;.$$

Принимая во внимание также соотношение Майера, окончательно получим

$$\frac{Q_{12}}{\mid Q_{23}\mid} \ =\ \frac{3,5\,R}{2\,(5/2\,R\,+\,R)} \ =\ 0,5\;.$$

3.11. Пусть величины давления и объема получают в адиабатическом процессе малые приращения: $\Delta p \ll p$ , $\Delta V \ll V$, тогда, в соответствии с уравнением Пуассона,

$$p\,V^\gamma =(p+\Delta p)(V+\Delta V )^\gamma = p\,V^\gamma \... ... p\over p} \right) \left(1 +{\Delta V\over V} \right)^\gamma\;.$$

Преобразуем данное равенство, применяя к $(1+\Delta V/ V)^\gamma$ формулу бинома и пренебрегая малыми величинами выше первого порядка:

$$\left(1 +{\Delta V\over V} \right)^\gamma\ \approx\ 1\ +\ \gamma\ {\Delta V\over V}\;\;;$$

$${\Delta p\over p}\ +\ \gamma\ {\Delta V\over V}\ =\ 0\;\;.$$ (21)

Это равенство устанавливает соотношение между малыми приращениями давления и объема при заданных $p$ и $V$ в адиабатическом процессе. Оно эквивалентно уравнению Пуассона.

Получим теперь связь между $\Delta p$, $\Delta V$, $p$ и $V$ в адиабатическом процессе, исходя из уравнения состояния идеального газа и первого начала термодинамики. Все вычисления будем проводить для одного моля идеального газа.

Из уравнения состояния имеем

$$p\,V\ =\ R\,T\;\;\;\; ;\;\;\;\;(p+\Delta p)(V+\Delta V )\ =\ R\,(T+\Delta T)\;\;,$$

откуда с точностью до малых первого порядка

$$V\,\Delta p\ +\ p\,\Delta V\ =\ R\,\Delta T\;\;.$$ (22)

В адиабатическом процессе внутренняя энергия уменьшается за счет совершенной работы:

$$\Delta U\ =\ C_v\,\Delta T\ =\ -\,p\,\Delta V\;\;.$$

С учетом этого (22) принимает вид

$$V\,\Delta p\ +\ p\,\Delta V\,\left(1\, +\,{R\over C_v} \right)\ =\ 0$$ (23)

или, учитывая соотношение Майера: $C_p=C_v+R$,

$${\Delta p\over p}\ +\ {C_p\over C_v}\ {\Delta V\over V}\ =\ 0\;\;.$$ (24)

Сравнивая последнее равенство с (21), можно видеть, что уравнение Пуассона будет справедливо при $\gamma = C_p/C_v$. Его можно записать как в переменных $(p,V)$, так и в переменных $(T,V)$ (с учетом уравнения состояния идеального газа):

$$p\,V^\gamma\ =\ const\;\;;\;\;\;\;\;\;T\,V^{\gamma-1}\ =\ const\;\;.$$ (25)

3.12. В отличие от предыдущей задачи при выводе уравнения типа (21) из уравнения состояния идеального газа и первого начала термодинамики здесь нужно учитывать изменение внутренней энергии как за счет совершенной работы (уменьшение), так и за счет поглощенного тепла (увеличение)

$$\Delta U\ =\ C_v\,\Delta T\ =\ -\,p\,\Delta V\ +\ C\,\Delta T\;\;.$$

Это приводит к замене в (23) $C_v$ на $C_v - C$ в результате вместо (24) получаем

$${\Delta p\over p}\ +\ {{(C_p\,-\,C)}\over {(C_v\,-C)}}\ {\Delta V\over V}\ =\ 0\;\;.$$ (26)

При постоянном значении $C$ величина

$${{(C_p\,-\,C)}\over {(C_v\,-C)}}\ \equiv\ n$$ (27)

(показатель политропы) будет постоянной в течение всего процесса. С учетом этого, сравнивая (26) с (21) и принимая во внимание то, что (21) эквивалентно уравнению Пуассона, получаем для политропического процесса уравнения, отличающиеся от (25) заменой $\gamma$ на $n$:

$$p\,V^n\ =\ const\;\;;\;\;\;\;\;\;T\,V^{n-1}\ =\ const\;\;.$$ (28)

При $n=0$ (27) выполняется для $C=C_p$, а (28) соответствует уравнению изобарного процесса: $p = const$.

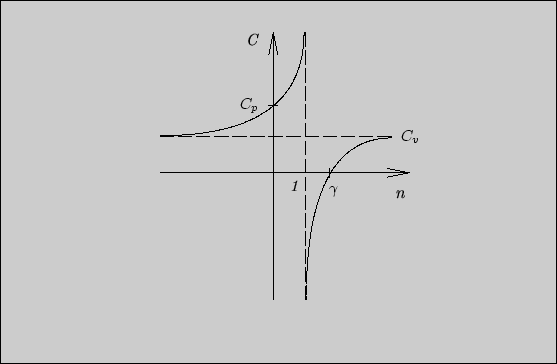
Рис. 24 

Условие $n=1$ для (27) означает $\vert C\vert\gg C_p$ и $\vert C\vert\gg C_v$, а с точки зрения (28) $n=1$ означает изотермический процесс: $pV = const$ или $T = const$. Изотермический процесс действительно соответствует бесконечной теплоемкости (плюс бесконечность при расширении, минус бесконечность - при сжатии).

При $n\to \pm\infty$ ($1/n \to 0$) согласно (27) $\ C=C_v\$, а (28) можно переписать в виде $\ p^{1/n}V = V = const$ - изохорный процесс.

Наконец, при $\ n=\gamma\$ (28) переходит в уравнение адиабаты, а (27) соответствует нулевому значению теплоемкости $C$.

Выразим из (27) теплоемкость $C$

$$C\,=\,C_v\,{(n-\gamma)\over (n-1)}$$

и построим зависимость этой функции от $n$, учитывая только что полученные результаты (рис. 24). Мы видим, что в области $1<n<\gamma$ теплоемкость отрицательна. Это означает, что в данном случае поглощение тепла сопровождается понижением температуры газа, а при выделении тепла температура повышается.

Этот, на первый взгляд, парадоксальный результат не противоречит первому началу термодинамики. Снижение температуры при поглощении тепла может быть обусловлено тем, что газ совершает работу, превышающую поглощенное тепло. Наоборот, если при сжатии над газом производится работа, превышающая выделенное тепло, то отдача тепла сопровождается нагреванием. Именно это и происходит в политропических процессах с $1<n<\gamma$.

Вопросы и задачи к разделу 5
"Второе начало термодинамики"

5.1. В общем случае нельзя говорить о постоянстве внутренней энергии в обратимом изотермическом процессе, однако в частных случаях это возможно, если между внутренней энергией и температурой имеется взаимно однозначное соответствие, например, это справедливо для идеального газа (см. вопрос 3.2.).

В соответствии со вторым началом термодинамики для обратимых процессов

$$\Delta S\ =\ \frac{\Delta Q}{T}\;.$$

В частности, в обратимом адиабатическом процессе
$\Delta S\,=\,0$.

Постоянство энтропии в обратимом адиабатическом процессе является прямым следствием второго начала термодинамики, поэтому имеет место в общем случае.

5.2. В обратимом адиабатическом процессе $\Delta S\,=\,0$. Поэтому на диаграмме $(T,S)$ адиабата изображается отрезком прямой, перпендикулярной оси $S$, а цикл Карно, таким образом, изображается прямоугольником (рис. 25).

Рис. 25 

Для тепловой машины направления процессов соответствуют обходу цикла по часовой стрелке, для холодильной машины - против часовой стрелки. Сравнивая определения элементарной полезной работы

$$\Delta A\ =\ p\,\Delta V$$

и тепла, поглощенного на малом участке обратимого процесса,

$$\Delta Q\ =\ T\,\Delta S\;,$$

можно видеть, что площадь под кривой процесса на диаграмме $(T,S)$ численно равна поглощенному теплу (или выделенному - в зависимости от направления процесса). В частности, для тепловой машины Карно тепло $Q_{1}$, поглощенное от нагревателя, равно площади прямоугольника $A{\it 12}B$, тепло $Q_{2}$, отданное холодильнику, равно площади прямоугольника $A{\it 43}B$ (см. рис. 25). Площадь прямоугольника 1234 равна разности $Q_{1}\,-\,Q_{2}$ и, следовательно, полезной работе, совершенной за цикл (как и на диаграмме $(p,V)$).

5.3. Если в начальном состоянии температуры газов различны, то процесс взаимной диффузии сопровождается необратимым теплообменом, который, как мы знаем, дает положительный вклад в энтропию системы. Поэтому рассмотрение вопроса достаточно ограничить случаем, когда начальные температуры газов одинаковы. Если газы считать идеальными, то при равенстве начальных температур их конечные состояния после достижения равновесия в системе в отсутствие химического взаимодействия будут такими же, как если бы каждый из газов расширялся в пустоту.

Действительно, парциальное давление каждого из газов в равновесии должно быть одинаковым по всему объему системы и по закону Дальтона для идеальных газов должно давать независимый вклад в суммарное давление смеси. Следовательно, в смеси химически не взаимодействующих идеальных газов каждая из компонент в равновесном состоянии ведет себя таким образом, как если бы другие компоненты отсутствовали.

Рассматривая энтропию смеси газов как сумму энтропий компонент, приходим к выводу, что, поскольку энтропия каждой из компонент в процессе диффузии увеличивается (так же, как и при расширении в пустоту), возрастает и суммарная энтропия.

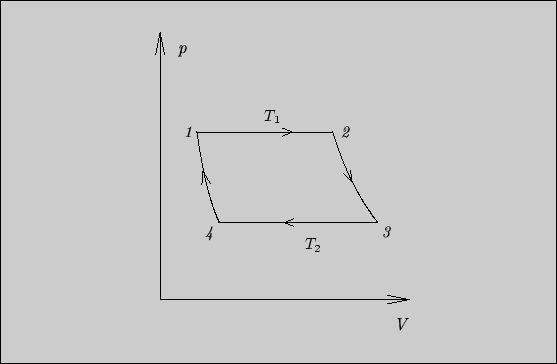
Рис. 26 

Учет неидеальности газов может привести к небольшим поправкам в значениях конечных параметров, но не может качественно изменить результаты протекания процесса.

Рассмотренный процесс является одним из примеров необратимого процесса в замкнутой системе, поэтому второе начало термодинамики определенно указывает на возрастание энтропии в таком процессе. Однако мы провели рассмотрение вопроса, не пользуясь законом возрастания энтропии, так же, как делали это при обосновании данного закона.

5.4. Такой цикл изображен на рис. 26. Изотермические участки одновременно являются изобарными, так как давление насыщенного пара при заданной температуре является фиксированной величиной. На изотерме $\it 1 \to \it 2$ происходит испарение. Тепло, необходимое для парообразования, поглощается от теплового резервуара с температурой $T_1$. На изотерме $\it 3 \to \it 4$ происходит конденсация. Выделенное тепло передается тепловому резервуару с температурой $T_2$.

Чтобы замкнуть цикл, адиабатическое сжатие нужно начинать до того, как вся испарившаяся вода сконденсируется изотермически (с выделением тепла в окружающую среду). Следовательно, на участке адиабатического сжатия $\it 4 \to \it 1$ конденсация пара продолжается, так как если всю воду, испарившуюся при расширении, сконденсировать на участке $\it 3 \to \it 4$, дальнейшее адиабатическое сжатие не приведет в состояние $\it 1$.

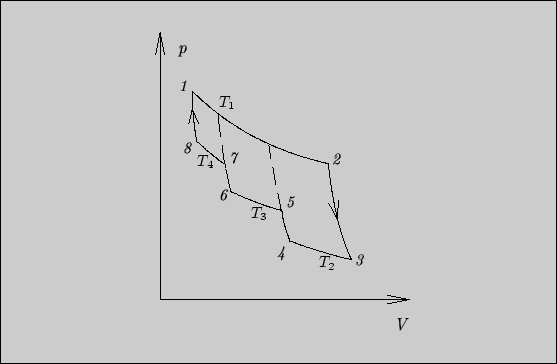
Рис. 27 

При адиабатическом сжатии тепло, освободившееся в процессе конденсации, не выделяется в окружающую среду, а расходуется на увеличение внутренней энергии системы, складываясь с внешней работой.

В отношении участка адиабатического расширения можно сказать, что он возможен без продолжения испарения, по крайней мере в том случае, если в состоянии $\it 2$ вся вода превратилась в пар.

Таким образом, действительно, тепло, освободившееся при конденсации пара, больше, чем тепло, затраченное на испарение, но часть тепла конденсации не отдается в окружающую среду, а остается в системе.

5.5. Продолжим адиабаты $\it 4 \to \it 5$, $\it 6 \to \it 7$ и $\it 8 \to \it 1$ до пересечения с изотермой $\it 1 \to \it 2$ (см. рис. 27). Рассматриваемый цикл будет эквивалентен последовательному прохождению трех циклов Карно, в каждом из которых выделяется тепло $Q$, а поглощаются три различные порции тепла:

$$Q_1^\prime = {T_1\over T_4}\ Q\;;\;\;\; Q_1^{\prime\prime} = ... ...}\ Q\;;\;\;\; Q_1^{\prime\prime\prime} = {T_1\over T_2}\ Q\;\;;$$

Полное выделенное тепло, таким образом, равно

$$Q_2 = 3\,Q\;\;,$$

а полное поглощенное тепло -

$$Q_1\ =\ Q_1^\prime + Q_1^{\prime\prime} + Q_1^{\prime\prime\p... ...\,T_1\ \left({1\over T_2} + {1\over T_3} + {1\over T_4} \right)$$

Отношение выделенного тепла к поглощенному равно

$${Q_2\over Q_1}\ =\ {3\,T_2\,T_3\,T_4\over {T_1\ (T_2 T_3 + T_2 T_4 + T_3 T_4)}}$$

Вопросы и задачи к разделу 6
"Первое и второе начала термодинамики в
теории тепловых машин"

6.1. Пусть две адиабаты пересекаются на диаграмме $(p,V)$ (рис. 28). Если осуществить между состояниями 3 и 1 на этих адиабатах изохорный процесс, как показано на рисунке, то получим цикл ${\it 1\rightarrow2\rightarrow3\rightarrow1}$, в котором совершается полезная работа, численно равная площади криволинейного треугольника 123. При этом теплообмен происходит только на участке

Рис. 28 

${\it 3\rightarrow1}$, где тепло поглощается. Таким образом, получаем вечный двигатель второго рода, что противоречит второму началу термодинамики. Следовательно, пересечение адиабат невозможно.

Второй вариант ответа. Как мы уже знаем, на диаграмме $(T,S)$ адиабаты изображаются параллельными прямыми, поэтому они не могут пересекаться. Отсутствие общих точек (общих состояний) на двух различных адиабатах позволяет заключить, что они не могут пересекаться и на любых других диаграммах.

6.2. Описанный рабочий цикл изображен на рис. 29. По условию промежуточные состояния на участках ${\it 2\rightarrow3}$ и ${\it 3\rightarrow1}$ при двух вариантах прохождения цикла одинаковы, значит, одинаковы и количества поглощенного и выделенного тепла. Таким образом, остается выяснить, в каком случае поглощается больше тепла на изотермическом участке цикла: при обратимом или необратимом его прохождении. Начальное состояние 1 и конечное состояние 2 изотермического участка для двух рассматриваемых случаев являются общими, поэтому приращение энтропии $\Delta S_{12}$ одинаково для обратимого и необратимого процессов. В соответствии со вторым началом термодинамики для обратимого изотермического процесса выполняется равенство

Рис. 29 

$$\Delta S_{12}\ =\ \frac{Q_{12}}{T}\;,$$

а для необратимого изотермического процесса - неравенство

$$\Delta S_{12}\ >\ \frac{Q^{\prime}_{12}}{T}\;,$$

где $T$ - температура на участке ${\it 1 \rightarrow 2}$. Отсюда

$$Q^{\prime}_{12}\ <\ T\,\Delta S_{12}\ =\ Q_{12}\;,$$

то есть тепло, поглощенное в необратимом изотермическом процессе, всегда меньше тепла, поглощенного в обратимом изотермическом процессе с теми же начальным и конечным состояниями. В частности, как нам известно, для необратимого изотермического расширения идеального газа в пустоту

$$Q^{\prime}_{12}\ =\ 0\;.$$

Здесь возникает попутный вопрос: не приводит ли полученный результат к тому, что к.п.д. необратимого цикла больше, чем к.п.д. обратимого цикла с теми же промежуточными состояниями на участках ${\it 2\rightarrow3}$ и ${\it 3\rightarrow1}$? Действительно, работа (площадь контура цикла на диаграмме $(p,V)$ одна и та же, а поглощенное тепло в необратимом цикле меньше. На самом деле это, конечно, не так, поскольку выражение для работы на элементарном участке

$$\Delta A\ =\ p\,\Delta V$$

и, следовательно, графический смысл работы как площади под кривой процесса на диаграмме $(p,V)$ имеют место только для обратимых процессов, так как только в этом случае давление в системе равно внешнему давлению (для необратимого процесса давление в промежуточных состояниях вообще может не иметь определенных значений). В частности, при расширении газа в пустоту работа вообще не совершается.

6.3. Как мы знаем, поглощенное тепло численно равно площади под кривой процесса на диаграмме $(T,S)$. Для данного цикла поглощенное и выделенное тепло соответственно равны

$$Q_{1}\ =\ Q_{12}\ =\ \frac{1}{2}\,(T_{2}\,+\,T_{1})(S_{2}\,-\,S_{1})\;,$$

$$Q_{2}\ =\ \mid Q_{31}\mid \ =\ T_{1}\,(S_{2}\,-\,S_{1})\;.$$

Отсюда, принимая во внимание, что $T_{2}\ =\ 3\,T_{1}$, для к.п.д. получаем

$$\eta\ =\ 1\ -\ \frac{Q_{2}}{Q_{1}}\ =\ 1\ -\ \frac{2\,T_{1}}{T_{2}\,+\,T_{1}}\ =\ 0,5\;.$$

6.4. В данном цикле тепло поглощается на изотермическом участке ${\it 1 \rightarrow 2}$ и выделяется на изохорном участке ${\it 2\rightarrow3}$. Максимальная температура достигается на изотерме, а минимальная - в состоянии 3. Количество выделенного тепла составляет

$$Q_{2}\ =\ \mid Q_{23}\mid \ =\ C_{v}\,\Delta T\;.$$

Поглощенное тепло определяется как сумма выделенного тепла и полезной работы:

$$Q_{1}\ =\ A\ +\ C_{v}\,\Delta T\;.$$

С учетом этого для к.п.д. получаем

$$\eta\ =\ \frac{A}{Q_{1}}\ =\ \frac{A}{A\,+\,C_{v}\,\Delta T}\;\;.$$

6.5. Работа, совершаемая в обратимом цикле, может быть выражена через поглощенное тепло следующим образом:

$$A\ =\ \eta\,Q_{1}\;,$$

где $\eta$ - к.п.д. цикла. Тогда искомое отношение работ равно отношению к.п.д. цикла Карно с теми же наибольшей и наименьшей температурами к к.п.д. рассматриваемого цикла, так как по условию количество поглощенного тепла в обоих циклах одинаково:

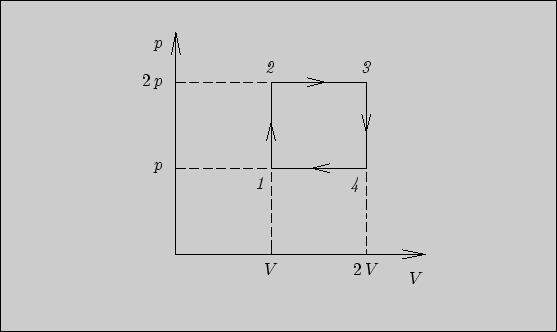
Рис. 30 

$$\frac{A_{\text{к}}}{A}\ =\ \frac{\eta_{\text{к}}}{\eta}\;\;.$$

Изобразим рассматриваемый
цикл на диаграмме $(p,V)$ (рис. 30). Совершаемая в цикле работа равна

$$A\ =\ (2\,p\,-\,p)(2\,V\,-\,V)\ =\ p\,V\;,$$

а поглощенное тепло -

$$Q_{1}\ =\ Q_{12}\,+\,Q_{23}\;;$$

$$Q_{1}\ =\ \nu\,C_{v}\,(T_{2}\,-\,T_{1}) \ +\ \nu\,C_{p}\,(T_{3}\,-\,T_{2})\;,$$

где $\nu$ - количество молей газа. Температуры $T_{1}$, $T_{2}$ и $T_{3}$ легко находятся из уравнения состояния идеального газа:

$$T_{1}\ =\ \frac{p\,V}{\nu\,R}\;\;,\qquad T_{2}\ =\ \frac{2\,p\,V}{\nu\,R}\;\;,\qquad T_{3}\ =\ \frac{4\,p\,V}{\nu\,R}\;\;,$$

причем очевидно, что $T_{1}$ является минимальной, а $T_{3}$ - максимальной температурами цикла.

Подставляя значения температур в выражение для $Q_{1}$, учитывая соотношение Майера и значение теплоемкости $C_{v}$, получаем

$$Q_{1}\ =\ \frac{13}{2}\ p\,V\;.$$

Отсюда к.п.д. рассматриваемого цикла получается равным

$$\eta\ =\ {A\over Q_1}\ =\ \frac{2}{13}\;.$$

К.п.д. цикла Карно с теми же предельными температурами равен

$$\eta_{\text{к}}\ =\ \frac{T_{3}\,-\,T_{1}}{T_{3}}\ =\ \frac{3}{4}\;,$$

а искомое соотношение -

$$\frac{A_{\text{к}}}{A}\ =\ \frac{39}{8}\ \approx\ 4,88\;.$$

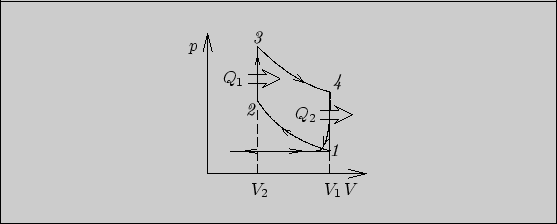
Рис. 31 

6.6. Цикл Отто (см. рис. 31) приближенно описывает работу карбюраторного двигателя внутреннего сгорания. Изобарный участок, примыкающий к состоянию 1, соответствует при расширении - всасыванию горючей смеси, при сжатии - выхлопу отработанных газов. После всасывания и сжатия рабочая смесь воспламеняется искрой (состояние 2) и сгорает, выделяя тепло $Q_1$. Процесс сгорания происходит достаточно быстро, поэтому приближенно описывается изохорой ${\it 2\to 3}$. Участок ${\it 3\to 4}$ описывает рабочий ход поршня после сгорания топлива. Участок ${\it 4\to 1}$ в реальном двигателе отсутствует. После открытия клапана в состоянии 4 давление выхлопных газов быстро падает до атмосферного и происходит выхлоп. Этот процесс приближенно показан кривой, начинающейся в состоянии 4. Однако после всасывания горючей смеси система возвращается в состояние 1. Таким образом, реальный процесс "выхлоп - всасывание" можно заменить изохорным охлаждением ${\it 4\to 1}$ с выделением тепла $Q_2$.

Поглощенное тепло $Q_1$ равно

$$Q_1\ = \ C_v\, (T_3\, -\, T_2)\;,$$

выделенное тепло (по абсолютной величине) -

$$Q_2\ =\ C_v\, (T_4\, -\, T_1)\;.$$

Для к.п.д., согласно (14), имеем

$$\eta\ =\ 1\ -\ {Q_2\over Q_1}\ =\ 1\ -\ {{T_4-T_1}\over {T_3-T_2}}\;.$$

Из уравнения адиабаты идеального газа ${\it 1\to 2}$

$$T_1\, V_1^{\gamma -1}\ =\ T_2\, V_2^{\gamma -1}\;,\phantom{AA... ...box{или} \phantom{AAA} T_2\ =\ T_1\, \varepsilon^{\gamma -1}\;.$$

Аналогично для адиабаты ${\it 3\to 4}$

$$T_3\, V_2^{\gamma -1}\ =\ T_4\, V_1^{\gamma -1}\;,\phantom{AA... ...box{или} \phantom{AAA} T_3\ =\ T_4\, \varepsilon^{\gamma -1}\;.$$

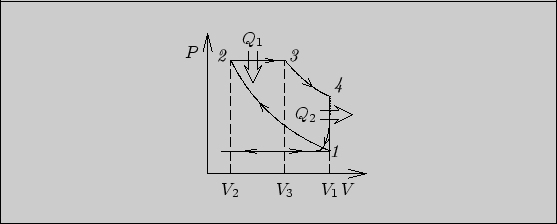
Рис. 32 

Окончательно для к.п.д. цикла Отто находим

$$\eta = 1 - {1\over \varepsilon^{\gamma -1}}\;.$$ (29)

Повышение к.п.д. карбюраторного двигателя, согласно (29), возможно за счет увеличения степени сжатия. Однако увеличение $\varepsilon$ ограничено, так как при сильном адиабатическом сжатии горючей смеси ее температура может повыситься настолько, что самовозгорание произойдет до того, как поршень достигнет положения, соответствующего минимальному объему газа в цилиндре.

6.7. На рис. 32 изображена диаграмма цикла Дизеля, приближенно описывающая работу дизельного двигателя. В цилиндр дизельного двигателя всасывается и подвергается адиабатическому сжатию (${\it 1\to 2}$) чистый воздух. Поэтому ограничение на степень сжатия накладывается лишь прочностью цилиндра. В состоянии 2 в рабочий объем из форсунки впрыскивается дизельное топливо, причем температура воздуха в состоянии 2 оказывается достаточно высокой для самовозгорания рабочей смеси. Горение дизельного топлива считается относительно медленным, так что поршень успевает смещаться и процесс горения приближенно описывается изобарой ${\it 2\to 3}$. Адиабата ${\it 3\to 4}$ и изохора ${\it 4\to 1}$ соответствуют рабочему ходу поршня и возврату в начальное состояние с выделением тепла $Q_2$ (в отношении реального процесса выхлопа справедливо то же, что сказано в решении предыдущей задачи).

Поглощенное в изобарном процессе тепло

$$Q_1\ =\ C_p\, (T_3\, -\, T_2)\;,$$

выделенное тепло

$$Q_2\ =\ C_v\, (T_4\, -\, T_1)\;.$$

К.п.д. цикла, таким образом, равно

$$\eta\ =\ 1\ -\ {Q_2\over Q_1}\ =\ 1\ -\ {{T_4-T_1}\over {\gam... ... =\ 1\ -\ {{T_4/T_1 -1}\over {\gamma\, (T_3/T_1 - T_2/T_1)}}\;.$$

Для адиабаты идеального газа ${\it 1\to 2}$, как и в цикле Отто, имеем

$${T_2\over T_1}\ =\ \varepsilon^{\gamma -1}\;,$$

для адиабаты ${\it 3\to 4}$ -

$${T_3\over T_4}\ =\ \left({V_1\over V_3}\right)^{\gamma - 1} =... ...amma -1} =\ \left({\varepsilon\over \rho}\right)^{\gamma -1}\;,$$

для изобары ${\it 2\to 3}$, в соответствии с уравнением состояния идеального газа

$${T_3\over T_2}\ =\ {V_3\over V_2}\ =\ \rho\;.$$

Отсюда получаем отношения температур, необходимые для вычисления к.п.д. цикла Дизеля:

$${T_3\over T_1}\ =\ {T_3\over T_2}\ {T_2\over T_1}\ =\ \rho\, \varepsilon^{\gamma -1}\;;$$

$${T_4\over T_1}\ =\ {T_4\over T_3}\ {T_3\over T_2}\ {T_2\over ... ...ht)^{\gamma -1} \rho\, \varepsilon^{\gamma -1} = \rho^\gamma\;.$$

Подставляя отношения температур в выражение для к.п.д., окончательно получаем

$$\eta\ =\ 1\ -\ {{\rho^\gamma - 1}\over {\gamma\,\varepsilon^{\gamma -1}\,(\rho-1)}}\;.$$ (30)

К.п.д. двигателя Дизеля, в соответствии с (30), повышается при увеличении степени сжатия. Как уже говорилось, степень сжатия в дизельном двигателе может быть значительно больше, чем в карбюраторном двигателе, поскольку она не ограничена пределом самовозгорания рабочей смеси. Однако при увеличении степени сжатия повышается давление в цилиндре двигателя и, соответственно, требуется более прочный цилиндр. Поэтому, наращивая к.п.д. за счет увеличения степени сжатия, мы должны одновременно увеличивать прочность (и, следовательно, массу) двигателя.

Увеличить к.п.д. дизельного двигателя, согласно (30), можно также при уменьшении степени предварительного расширения. Действительно, отношение $(\rho^\gamma - 1)/(\rho-1)$ уменьшается при снижении $\rho$, что приводит к увеличению к.п.д. Степень предварительного расширения будет уменьшаться при сокращении порции топлива, впрыскиваемого в рабочий объем в каждом цикле. Однако при этом уменьшается и мощность двигателя (сокращается площадь внутри контура цикла на диаграмме ($p,V$) и, следовательно, уменьшается полезная работа в каждом цикле).

Оптимальный режим работы дизельного двигателя определяется компромиссом между увеличением к.п.д. за счет повышения степени сжатия и нежелательным наращиванием массы двигателя, а также между увеличением к.п.д. за счет снижения $\rho$ и одновременным снижением мощности.

6.8. Доказательство эквивалентности двух утверждений означает доказательство того, что из первого утверждения следует второе, а из второго - первое. Заметим, что если невыполнение утверждения $''\!\!A''$ неминуемо приводит к невыполнению утверждения $''\!B''$, то это означает, что из $''\!B''$ следует $''\!\!A''$, так как если бы $''\!\!A''$ в этом случае не следовало из $''\!B''$, то его нарушение могло бы иметь место и при выполнении $''\!B''$.

Докажем вначале эквивалентность принципа Томсона и принципа Клаузиуса. Пусть нарушен принцип Клаузиуса. В этом случае возможен процесс, единственным результатом которого была бы передача тепла от холодного тела к горячему. Рассмотрим процесс, в котором тепло $Q_2$ передается от теплового резервуара с температурой $T_2$ к тепловому резервуару с температурой $T_1$ ($T_1>T_2$) без других изменений в системе. Проведем между этими термостатами цикл Карно, в котором тепло $Q_1+Q_2$ поглощается от горячего термостата, а холодному отдается тепло $Q_2$. В результате последовательности этих двух процессов для холодного резервуара сумма отданного и полученного тепла равна нулю, горячий резервуар получает тепло $Q_2$, а отдает $Q_1+Q_2$, то есть в сумме отдает тепло $Q_1$, которое, в соответствии с первым началом термодинамики, идет на совершение равной ему работы $A$. При этом никаких изменений в системе, кроме полного преобразования тепла $Q_1$ в работу, не происходит. Мы могли бы осуществлять этот процесс циклически, подобрав параметры цикла Карно таким образом, чтобы передаваемое холодному резервуару тепло в каждый промежуток времени в точности компенсировало тепло, самопроизвольно передаваемое от холодного термостата к горячему. Это означает возможность построения вечного двигателя второго рода, что противоречит принципу Томсона. Таким образом, принцип Клаузиуса является следствием принципа Томсона.

Пусть теперь нарушен принцип Томсона. Тогда возможна циклически действующая машина, полностью преобразующая поглощенное тепло в работу. Возьмем машину, которая в каждом цикле поглощает от термостата тепло $Q_1$ и производит равную ему работу. Используем эту работу в качестве внешней для обратного цикла Карно, в котором тепло $Q_2$ поглощается от другого, более холодного, термостата, а первому термостату отдается тепло $Q_1+Q_2$. Легко понять, что суммарным результатом такого процесса будет передача тепла $Q_2$ от холодного тела к горячему, причем результат этот будет единственным, так как обе машины совершили полный цикл и вся произведенная первой машиной работа затрачена на приведение в действие второй машины. Тем самым нарушен принцип Клаузиуса. Это означает, что из принципа Клаузиуса следует принцип Томсона. Эквивалентность этих двух формулировок второго начала термодинамики доказана.

Рис. 33 

В разделе 5.3 мы получили принцип энтропии как прямое следствие постулата Клаузиуса. Далее было доказано (см. раздел 6, с. [перейти]), что принцип
Томсона следует из принципа энтропии. Доказав эквивалентность принципов Клаузиуса и Томсона, мы можем представить наши результаты в виде схемы (см. рис. 33). Двигаясь на схеме по стрелкам, указывающим направления логических следствий, мы можем от любого из принципов прийти к любому другому, что и означает их эквивалентность.

Вопросы и задачи к разделу 7
"Холодильные машины"

7.1. При более высокой температуре в помещении холодильник потребляет больше электроэнергии по двум причинам.

Первая из них связана с тем, что выброс избытка энтропии в окружающую среду при более высокой температуре требует выделения большего количества тепла. Поэтому для извлечения фиксированного количества тепла из морозильной камеры требуется большая внешняя работа

$$A_{\text{вн}}\ =\ Q_{1}\,-\,Q_{2}\;,$$

а источником внешней работы как раз и является энергия, потребляемая из электрической сети.

Вторая причина связана с тем, что при более высокой температуре окружающего воздуха интенсивнее идет процесс просачивания тепла внутрь холодильника, и для поддержания фиксированной температуры в морозильной камере (а именно на этот показатель настраивается работа реле, включающего и выключающего компрессор) требуется большая продолжительность работы компрессора по отношению ко времени остановки.

Поясним сказанное количественно, считая, что в холодильной машине реализуется обратимый цикл Карно. Тогда если температура в помещении - $T_{1}$, а температура в морозильной камере - $T_{2}$, то

$$Q_{1}\ =\ \frac{T_{1}}{T_{2}}\,Q_{2}\;\;,\;\;\;\;\mbox{и}\;\;... ...\text{вн}}\ =\ \left(\frac{T_{1}}{T_{2}}\;-\;1\right)\,Q_{2}\;.$$

При фиксированной температуре $T_{2}$ возрастание $T_{1}$ приводит к увеличению отношения $T_{1}/T_{2}$, что соответствует первой из названных выше причин увеличения $A_{\text{вн}}$. Вторая причина связана непосредственно с увеличением второго сомножителя - $Q_{2}$ в формуле для $A_{\text{вн}}$ (на самом деле отбираемое за один цикл тепло определяется температурой $T_{2}$, поэтому следует говорить не об увеличении $Q_{2}$, а об увеличении продолжительности работы двигателя по отношению ко времени остановки).

7.2. Тепло, поглощаемое рабочим телом холодильной машины при замерзании воды в морозильной камере, равно

$$Q_{2}\ =\ q_{2}\,m_{2}\;,$$

где $q_{2}$ - удельная теплота плавления воды, $m_{2}$ - масса замороженной воды. Тепло, отдаваемое рабочим телом при испарении воды в кипятильнике, равно

$$Q_{1}\ =\ q_{1}\,m_{1}\;,$$

где $q_{1}$ - удельная теплота парообразования, $m_{1}$ - масса испарившейся воды. Для идеального цикла Карно справедливо соотношение

$$\frac{Q_{1}}{Q_{2}}\ =\ \frac{T_{1}}{T_{2}}\;\;,$$

где $T_{1}$ и $T_{2}$ - абсолютные температуры соответственно горячего и холодного тепловых резервуаров. Отсюда получается искомая масса льда

$$m_{2}\ =\ \frac{Q_{2}}{q_{2}}\ =\ \frac{Q_{1}\,T_{2}}{q_{2}\,... ...frac{q_{1}\,T_{2}}{q_{2}\,T_{1}}\ \approx\ 14,85\ \text{ кг}\ .$$

Вопросы и задачи к разделу 8
"Замечательные задачи"

8.1. Объем вытесненного телом воздуха ( $10^{-3}\ \text{м}^{3}$) ничтожно мал по сравнению с объемом воздуха в комнате ( $60\ \text{м}^{3}$), поэтому мы пренебрежем уменьшением объема и массы воздуха в комнате в результате внесения тела.

Температуру $T^{\prime}$, установившуюся в результате теплообмена между воздухом в комнате и телом, можно определить из уравнения теплового баланса:

$$\rho\,V\,c_{p}\,(T-T^{\prime})\ =\ \rho_{1}\,V_{1}\,c_{1}\, (T^{\prime}-T_{1})\;,$$

где $V$ и $T$ - объем и начальная температура воздуха, $V_{1}$ и $T_{1}$ - объем и начальная температура тела. Уравнение выражает равенство тепла, отданного воздухом, и тепла, поглощенного телом.

Мы знаем, что при постоянном атмосферном давлении произведение массы воздуха в комнате на его температуру - величина постоянная. Поэтому при охлаждении воздуха в комнате будет увеличиваться его масса за счет притока воздуха из внешней среды. Строго говоря, это обстоятельство нужно было бы учесть в уравнении теплового баланса, что привело бы к появлению дополнительного слагаемого в левой части уравнения, соответствующего тепловому вкладу пришедшего извне воздуха (это можно сделать, если дополнительно задать температуру наружного воздуха). Однако реально, как можно предположить (и мы в этом убедимся), температура воздуха и, следовательно, его масса изменяются незначительно. Поэтому для вычисления $T^{\prime}$ воспользуемся уже записанным уравнением:

$$T^{\prime}\ =\ \frac{\rho\,V\,c_{p}\,T\ + \ \rho_{1}\,V_{1}\,... ...ho\,V\,c_{p}\ +\ \rho_{1}\,V_{1}\,c_{1}} \ \approx\ 292,3\ K\;.$$

Таким образом, температура воздуха в комнате уменьшается примерно на $0,7\ K$, а температура тела увеличивается на $12,3\ K$. Поскольку работы в процессе нагрева тела не совершается, все переданное ему тепло идет на увеличение его внутренней энергии:

$$\Delta U\ =\ \rho_{1}\,V_{1}\,c_{1}\,(T^{\prime}-T_{1}) \ \approx\ 51,7\ \text{ кДж}\;,$$

а так как внутренняя энергия воздуха в комнате при постоянном атмосферном давлении остается постоянной (не зависит от температуры), прирост внутренней энергии тела осуществляется за счет внутренней энергии пришедшего извне воздуха и работы по его сжатию. Убедимся в этом.

Из постоянства произведения массы воздуха в комнате на его температуру имеем

$$\frac{m^{\prime}}{m}\ =\ \frac{T}{T^{\prime}}\;\;,$$

где $m=\rho\,V$ - начальная масса воздуха в комнате, $m^{\prime}$ - его масса после установления равновесия. Отсюда увеличение массы воздуха в комнате

$$\Delta m\ =\ m^{\prime}\,-\,m\ =\ \rho\,V\, \frac{T-T^{\prime}}{T^{\prime}}\;.$$

Внутренняя энергия пришедшего извне воздуха, если для простоты считать, что его температура совпадает с $T^{\prime}$, равна

$$\Delta U_{1}\ =\ \Delta m\,c_{v}\,T^{\prime} \ =\ \rho\,V\,c_{v}\,(T-T^{\prime})\;.$$

Внешняя работа по сжатию воздуха при его притоке в комнату определяется следующим образом:

$$A_{\text{вн}}\ =\ p_{0}\,(V^{\prime}-V)\ =\ \frac{\Delta m}{\mu} \ R\,T\;,$$

где $V^{\prime}$ - объем, занимаемый массой воздуха $m^{\prime}$ при температуре $T$ (здесь и в следующем выражении мы учитываем, что $(T-T^{\prime}) \ll T\approx T^{\prime}$). Принимая во внимание соотношение Майера для удельных теплоемкостей: $c_{p}-c_{v}\,=\,R/\mu$, в сумме получим

$$A_{\text{вн}}\,+\,\Delta U_{1}\ =\ \Delta m\,c_{p}\,T^{\prime... ...\ \rho\,V\,c_{p}\,(T-T^{\prime})\ \approx\ 51,6\ \text{ кДж}\;,$$

что совпадает с увеличением внутренней энергии тела.

Если температура наружного воздуха отличается от $T^{\prime}$, то результат изменяется несущественно, так как отличие температуры окружающей среды от $T^{\prime}$ в реальной ситуации все равно намного меньше, чем сама величина $T^{\prime}$. Однако следует заметить, что и в этом случае при внесении соответствующего уточнения в уравнение теплового баланса окажется, что прирост внутренней энергии тела в точности покрывается за счет внешней работы и внутренней энергии пришедшего извне воздуха.

8.2. Температура воды в отопительной системе поддерживается постоянной за счет того, что тепло, отдаваемое отапливаемому помещению, компенсируется теплом, поступающим в отопительную систему из высокотемпературного и низкотемпературного (природного) тепловых резервуаров. Таким образом, при неизменных условиях в отапливаемом помещении постоянным должно оставаться и тепло, поступающее в отопительную систему. Для динамической системы отопления это тепло, как мы знаем, выражается формулой (20):

$$Q\ =\ q\,m\,\frac{T_{2}\,(T_{1}-T_{0})}{T_{1}\,(T_{2}-T_{0})}\;.$$

Здесь $q$ и $m$ - соответственно удельная теплотворная способность и масса сожженного топлива, остальные обозначения совпадают с обозначениями в условии задачи. Выразим массу сожженного топлива через передаваемое тепло, теплотворную способность и температуры тепловых резервуаров

$$m\ =\ \frac{Q\,T_{1}\,(T_{2}-T_{0})}{q\,T_{2}\,(T_{1}-T_{0})}\;.$$

Аналогично выражается масса топлива $m^{\prime}$ при новой температуре природного резервуара $T^{\prime}_{0}\,=\,295\ K$ (значения остальных величин при этом остаются прежними). Тогда отношение масс равно

$$\frac{m}{m^{\prime}}\ = \ \frac{(T_{2}-T_{0})(T_{1}-T^{\prime}_{0})}{(T_{1}-T_{0})(T_{2}- T^{\prime}_{0})}\ \approx\ 1,32\;.$$

Таким образом, при повышении температуры природного резервуара с $280\ K$ до $295\ K$ потребление топлива для поддержания прежней температуры в отопительной системе можно уменьшить в 1,32 раза.

Далее: Об этом документе ... Вверх: Термодинамика Назад: 8.  Замечательные задачи